A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-CIRCLE -JEE Advanced (Single Correct Answer Type)
- Tangents drawn from the point P(1,8) to the circle x^2 +y^2 -6x -4y-11...
Text Solution
|
- The circle passing through the point (-1,0) and touching the y-axis at...
Text Solution
|
- The locus of the middle point of the chord of contact of tangents draw...
Text Solution
|
- Circle(s) touching x-axis at a distance 3 from the origin and having a...
Text Solution
|
- A circle S passes through the point (0, 1) and is orthogonal to the ci...
Text Solution
|
- Let RS be the diameter of the circle x^2+y^2=1, where S is the point (...
Text Solution
|
- Let T be the line passing through the points P(-2,\ 7) and Q(2,\ -5...
Text Solution
|
- A possible equation of L is (A) x 3y 1 (B) x 3y 1 (C) x 3y 1 (D) x...
Text Solution
|
- A tangent PT is drawn to the circle x^2+y^2=4 at the point P(sqrt3,1)....
Text Solution
|
- PARAGRAPH "X" Let S be the circle in the x y -plane defined by the eq...
Text Solution
|
- Let S be the circle in the x y -plane defined by the equation x^2+y^2=...
Text Solution
|
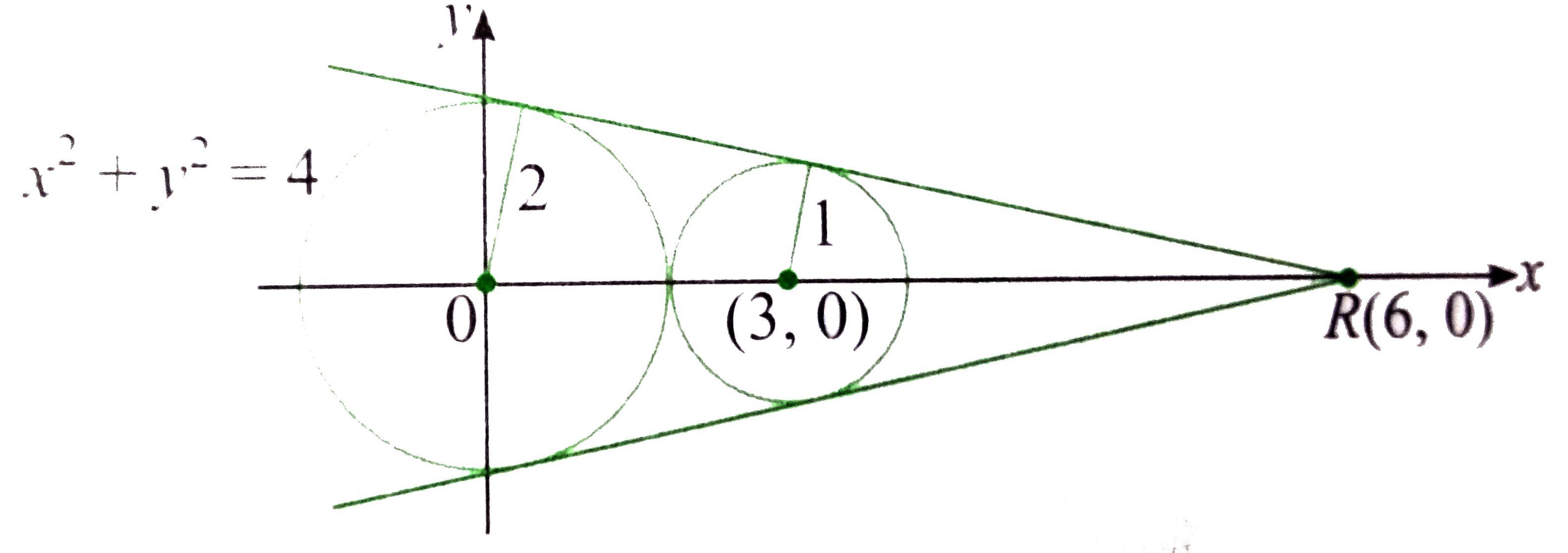
- The centres of two circles C(1) and C(2) each of unit radius are at a...
Text Solution
|
- The straight line 2x-3y = 1 divides the circular region x^2+ y^2 le6 i...
Text Solution
|
- For how many values of p, the circle x^2+y^2+2x+4y-p=0 and the coordin...
Text Solution
|