Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
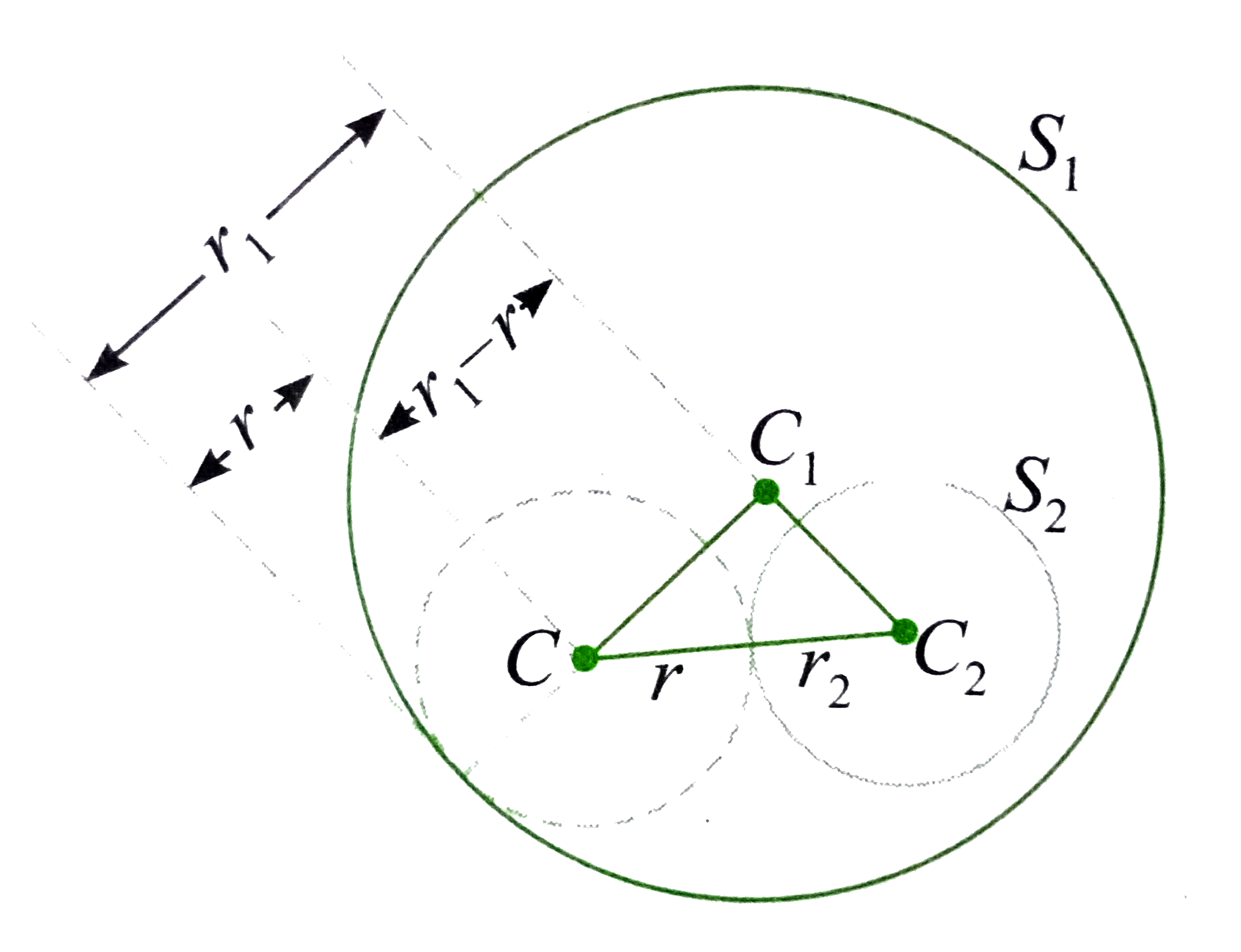
- Two circles are given such that one is completely lying inside the ...
Text Solution
|
- Two circles are given such that one is completely lying inside the ...
Text Solution
|
- Two circles are given such that they neither intersect nor touch. Then...
Text Solution
|
- Three circles,each of radius one,have centres at A,B and C. Circles A ...
Text Solution
|
- Prove that "in two concetric circles, a chord of the bigger circle , t...
Text Solution
|
- Two circles are given such that one is completely lying inside the ...
Text Solution
|
- Statement 1 : The locus of the center of a variable circle touching...
Text Solution
|
- Two circles are given such that they neither intersect nor touch. Then...
Text Solution
|
- उस वृत्त के केन्द्र का बिन्दुपथ, जो दो दिये गये वृत्तों को बाह्यत: स्प...
Text Solution
|