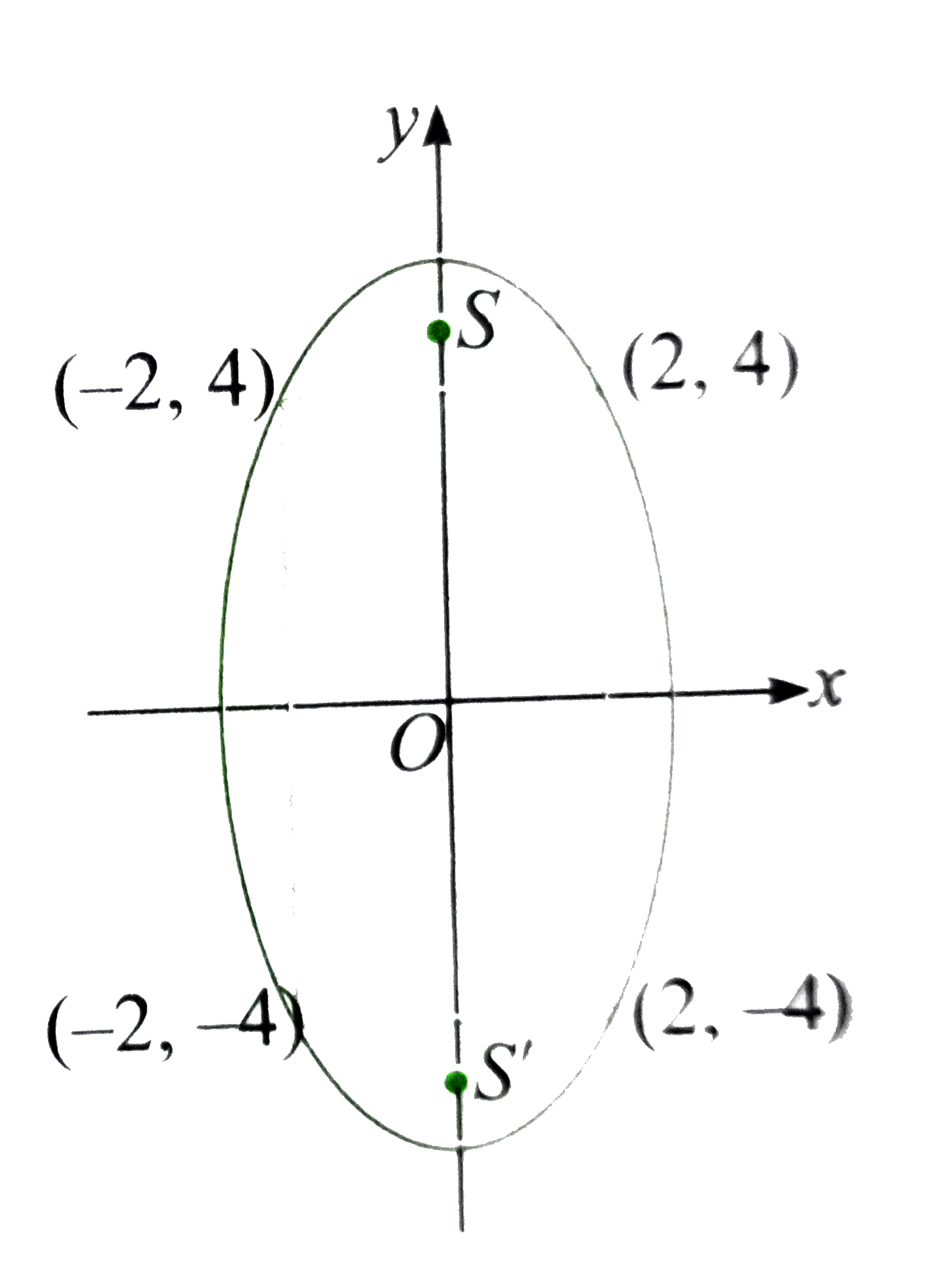
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An ellipse circumscribes a quadrilateral whose sides are given by x=-+...
Text Solution
|
- The eccentricity of an ellipse is 1/2 and the distance between its foc...
Text Solution
|
- The eccentricity of an ellipse is 1/2 and the distance between its foc...
Text Solution
|
- An ellipse circumscribes a quadrilateral whose sides are given by x=-+...
Text Solution
|
- If the latus rectum of an ellipse with major axis along y-axis and cen...
Text Solution
|
- उस दीर्घवृत्त का समीकरण ज्ञात कीजिए जिसकी दीर्घ अक्ष, x-अक्ष के अनुदिश...
Text Solution
|
- किसी दीर्घवृत्त की उत्केन्द्रता 1/2 है तथा नाभियों के बीच की दूरी...
Text Solution
|
- Area of the quadrilateral formed by the extremities of major axis and ...
Text Solution
|
- Taking major and minor axes as x and y - axes respectively , find the ...
Text Solution
|