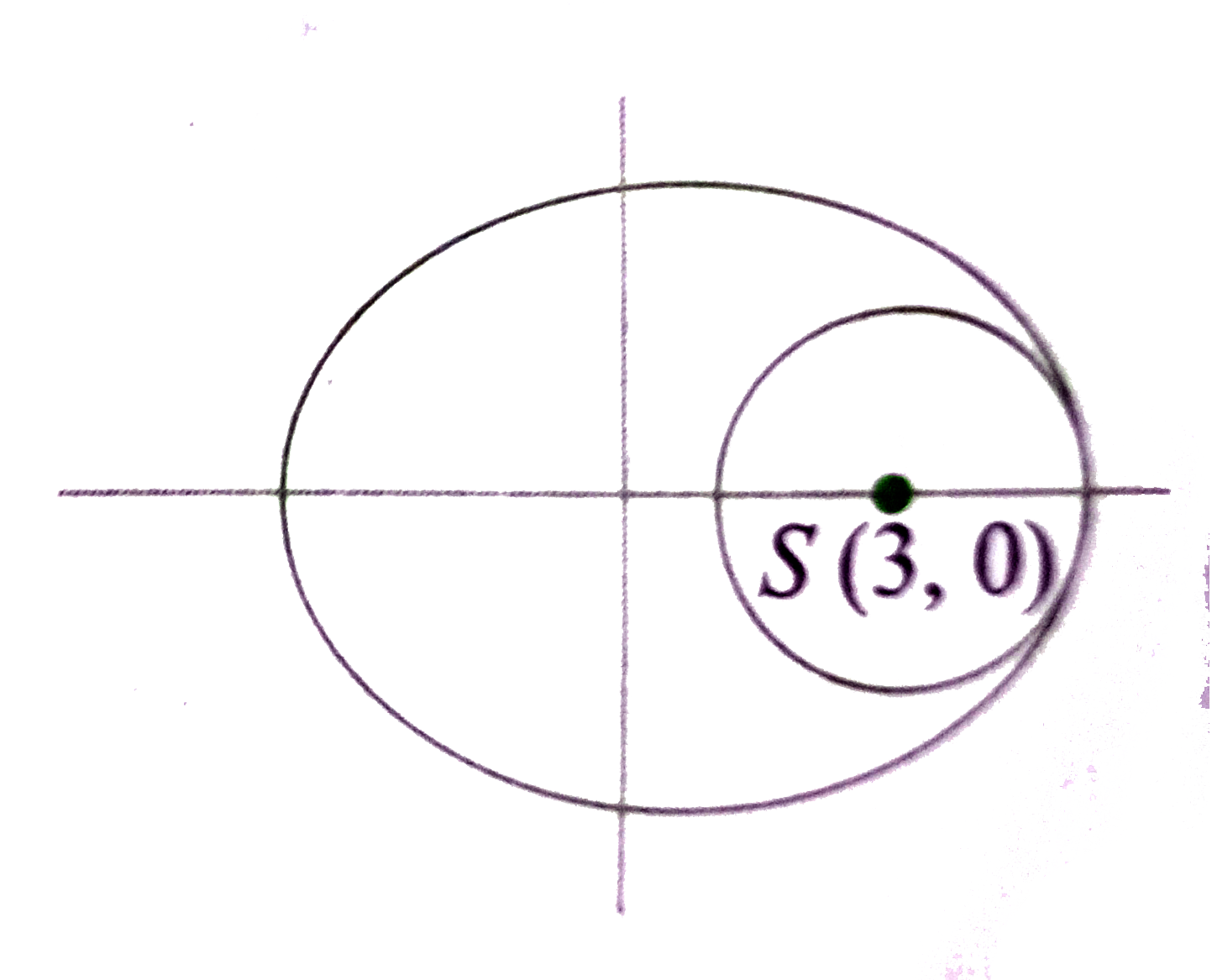Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An ellipse is drawn with major and minor axis of length 10 and 8 resp...
Text Solution
|
- An ellipse is drawn with major and minor axis of length 10 and 8 respe...
Text Solution
|
- An ellipse is cutout of a circle of radius a, the major axis of the el...
Text Solution
|
- An ellipse is drawn by taking a diameter of the circle (x-1)^(2) + ...
Text Solution
|
- The lengths of major and minor axis of an ellipse are 10 and 8 respect...
Text Solution
|
- दीर्घवृत के दीर्घ-अक्ष को व्यास मानकर खींचे गये वृत को दीर्घवृत का सहा...
Text Solution
|
- An ellipse is drawn by taking a diameter of the circle (x – 1)^2 + y^2...
Text Solution
|
- An ellipse sliding along coordinate axes.If the foci of ellipse are (1...
Text Solution
|
- An ellipse is drawn by taking the diameter of the circle (x-1)^(2)+y^(...
Text Solution
|