Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
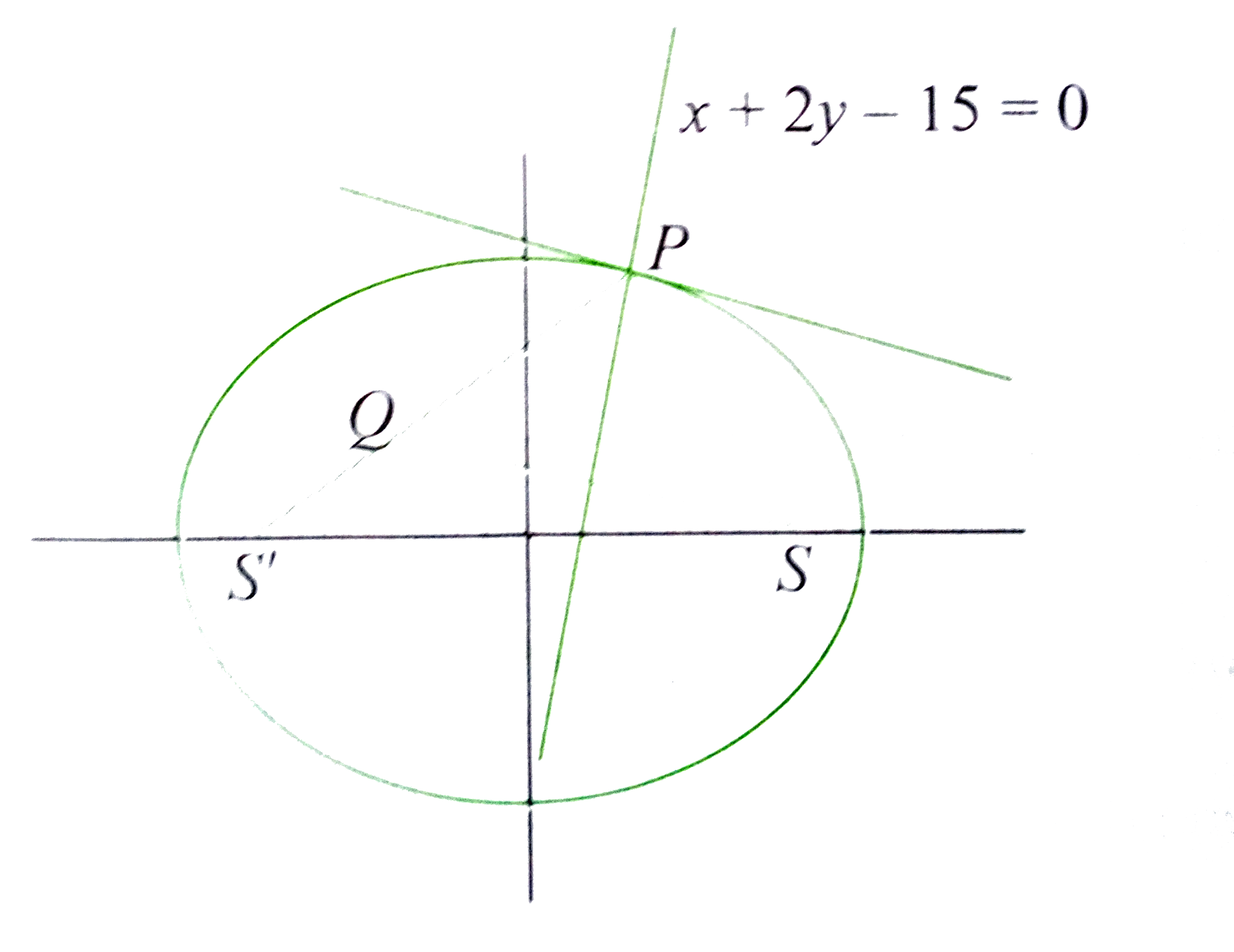
- The foci of an ellipse are S(3,1) and S'(11,5)The normal at P is x+2y-...
Text Solution
|
- If P is a point on the ellipse (x^(2))/(16)+y'(20)=1, whose foci are S...
Text Solution
|
- The foci of an ellipse are S(3,1) and S'(11,5) The normal at P is x+2y...
Text Solution
|
- If P is any point on the ellipse x^(2)/36 +y^(2)/16=1 and S and S', a...
Text Solution
|
- If P is any point on the ellipse 9x^(2) + 36y^(2) = 324 whose foci are...
Text Solution
|
- The tangent at any point P on a standard ellipse with foci as S & S' m...
Text Solution
|
- Find the equation of the ellipse whose length of major axis is 4 and l...
Text Solution
|
- Foci of an ellipse are at S(1,7),S'(1,-3) .The point P is on the ellip...
Text Solution
|
- If P is any point on the ellipse (x^(2))/(36) + (y^(2))/(16) = 1 , and...
Text Solution
|