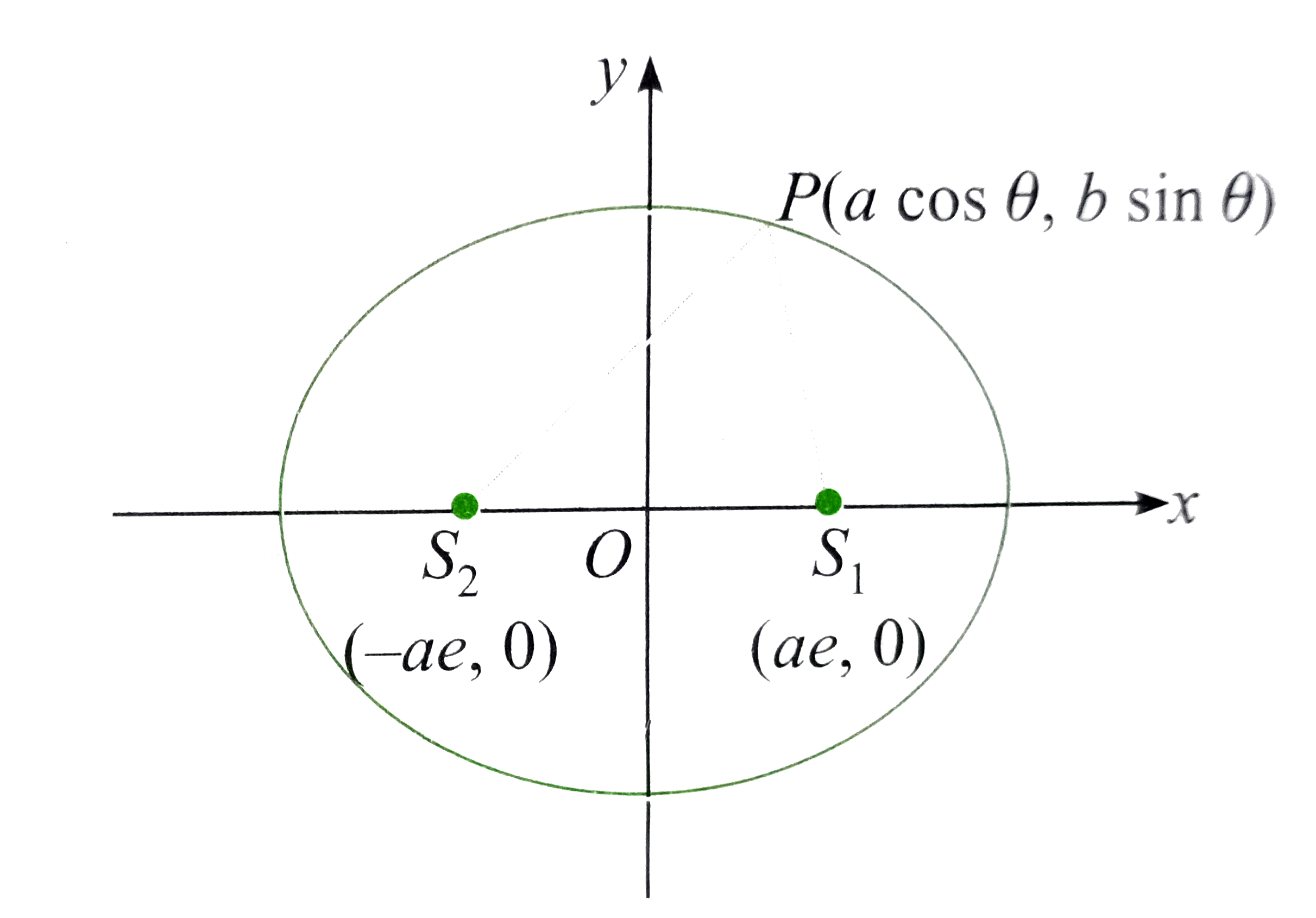
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let P be a pooint on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1(ag...
Text Solution
|
- If F1 and F2 are the feet of the perpendiculars from the foci S1a ...
Text Solution
|
- P is a variable point on the ellipse with foci S(1) and S(2). If A is ...
Text Solution
|
- If P is any point on the hyperbola ((x-1)^(2))/(9)-((y+1)^(2))/(16)=1 ...
Text Solution
|
- Let (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 and (x^(2))/(A^(2))-(y^(2))/(B^(...
Text Solution
|
- Let P be a pooint on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1(ag...
Text Solution
|
- If P is a point on the hyperbola 16x^(2) - 9y^(2) = 144 whose foci ar...
Text Solution
|
- If F(1), F(2), F(3) be the feet of the perpendicular from the foci S(1...
Text Solution
|
- Consider an ellipse (x^(2))/(13)+(y^(2))/(4)=1 and a variaote point P(...
Text Solution
|