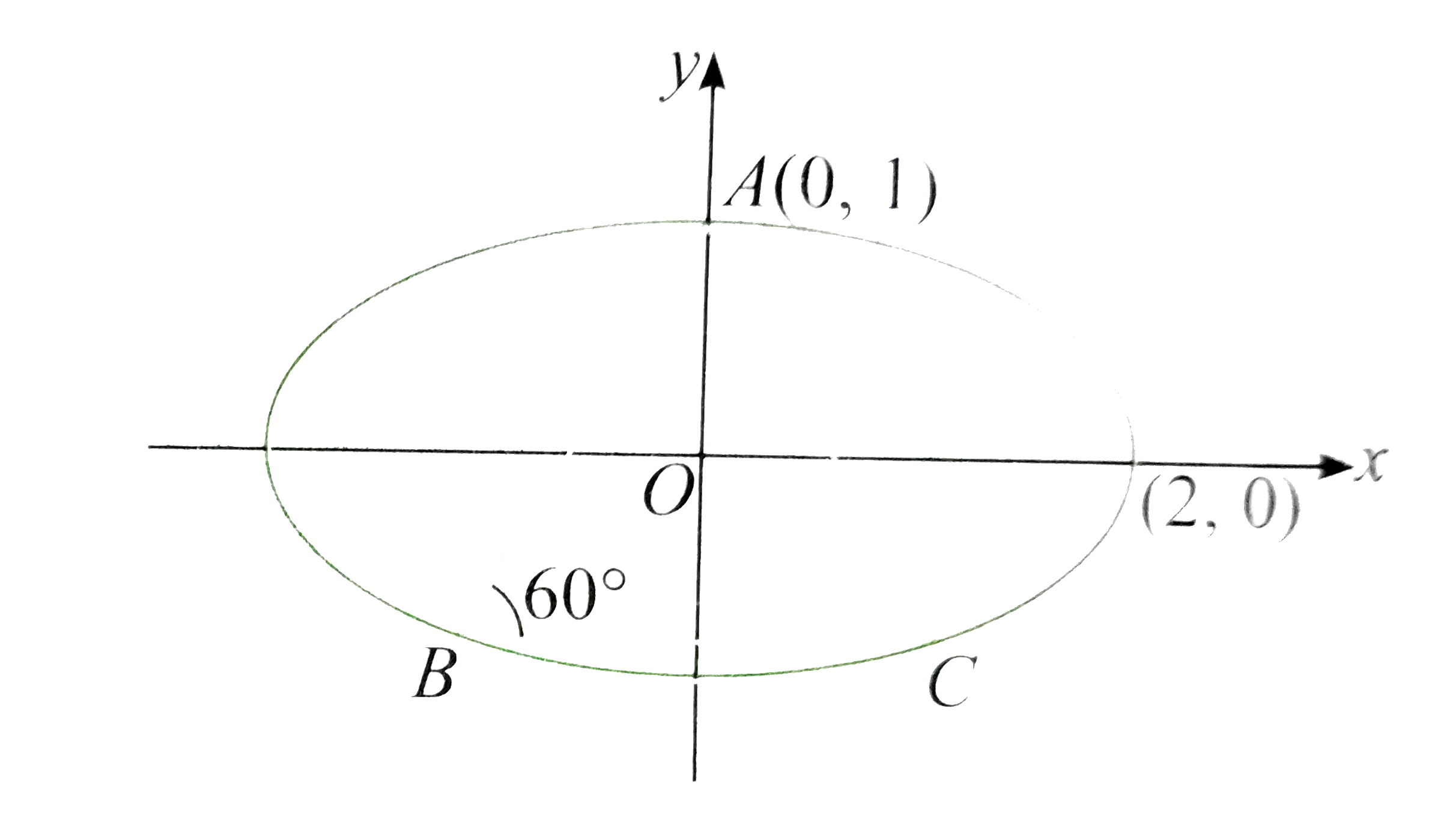
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An equilateral triangle is inscribed in an ellipse whose equation is x...
Text Solution
|
- An equilateral triangle is inscribed in the parabola y^2= 4 ax where ...
Text Solution
|
- An equilateral triangle is inscribed in an ellipse whose equation is x...
Text Solution
|
- An equilateral teiangle is inscribed in the parabola y^(2)=x whose one...
Text Solution
|
- An equilateral triangle is inscribed in the ellipse whose equation is ...
Text Solution
|
- An equilateral triangle is inscribed in the parbola y^(2)=4x one of w...
Text Solution
|
- y^2=x অধিবৃত্তে একটি সমবাহু ত্রিভজ অন্তরলিখিত হয় যার একটি শীর্ষ হল অধি...
Text Solution
|
- Express each of the following decimals in the p/q form 66.6
Text Solution
|
- An equilateral triangle is inscribed in the parabola y^(2)=4ax, where ...
Text Solution
|