A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
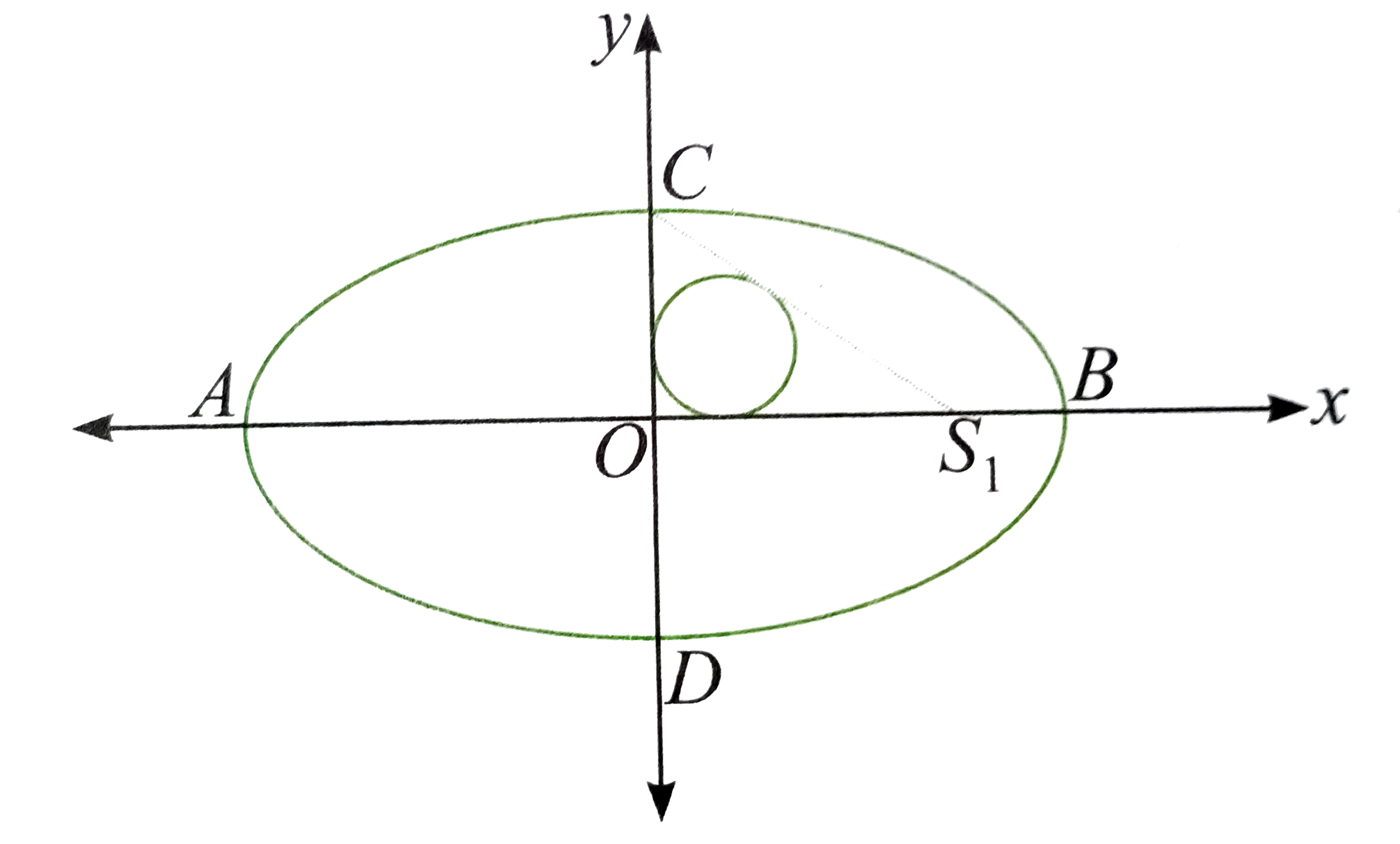
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- S(1),S(2), are foci of an ellipse of major axis of length 10 units and...
Text Solution
|
- Consider an ellipse E ,(x^2)/(a^2)+(y^2)/(b^2)=1 , centered at point O...
Text Solution
|
- An ellipse has the points (1,-1) and (2,-1) as its foci and x+y=5 as o...
Text Solution
|
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- An ellipse E,(x^(2))/(a^(2))+(y^(2))/(b^(2))=1, centred at point O has...
Text Solution
|
- Consider an ellipse E:x^(2)/a^(2)+y^(2)/b^(2)=1, centered at point 'O'...
Text Solution
|
- F is one of the foci of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 ...
Text Solution
|
- Consider an ellipse E ,(x^2)/(a^2)+(y^2)/(b^2)=1 , centered at point O...
Text Solution
|