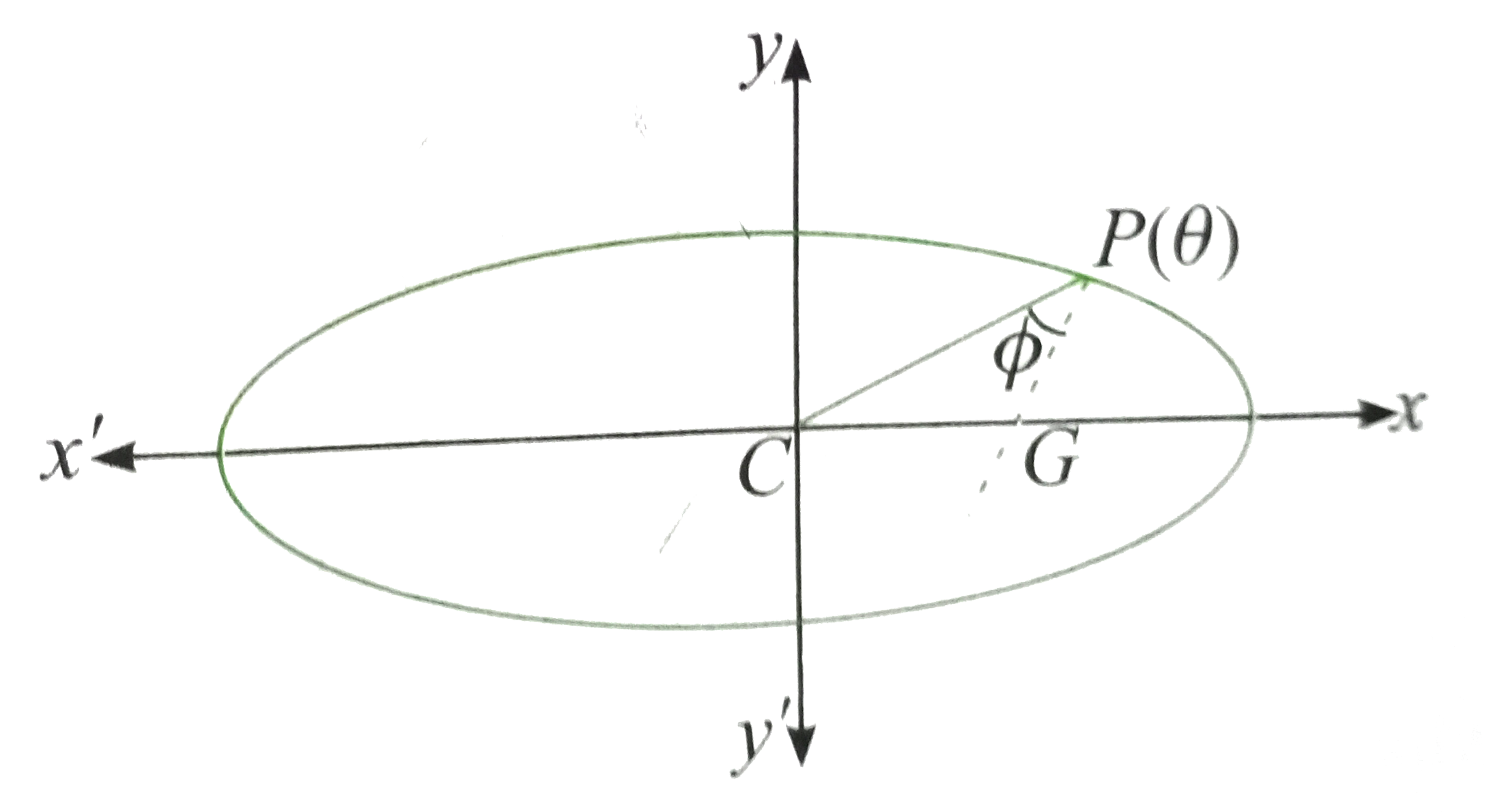
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Consider the ellipse whose major and minor axes are x-axis and y-axis,...
Text Solution
|
- Consider the ellipse whose major and minor axes are x-axis and y-axis,...
Text Solution
|
- The order of the differential equation of ellipse whose major and mino...
Text Solution
|
- Find the equation of the ellipse whose major axis is 8 and minor axis ...
Text Solution
|
- If the normal at any point P on the ellipse cuts the major and minor a...
Text Solution
|
- An ellipse hase semi-major of length 2 and semi-minor axis of length 1...
Text Solution
|
- The lengths of major and minor axis of an ellipse are 10 and 8 respect...
Text Solution
|
- Taking the major and minor axes as the axes of coordinates, find the e...
Text Solution
|
- Let P be a point on the ellipse (x^(2))/(16) + (y^(2))/(9) = 1 . If...
Text Solution
|