A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
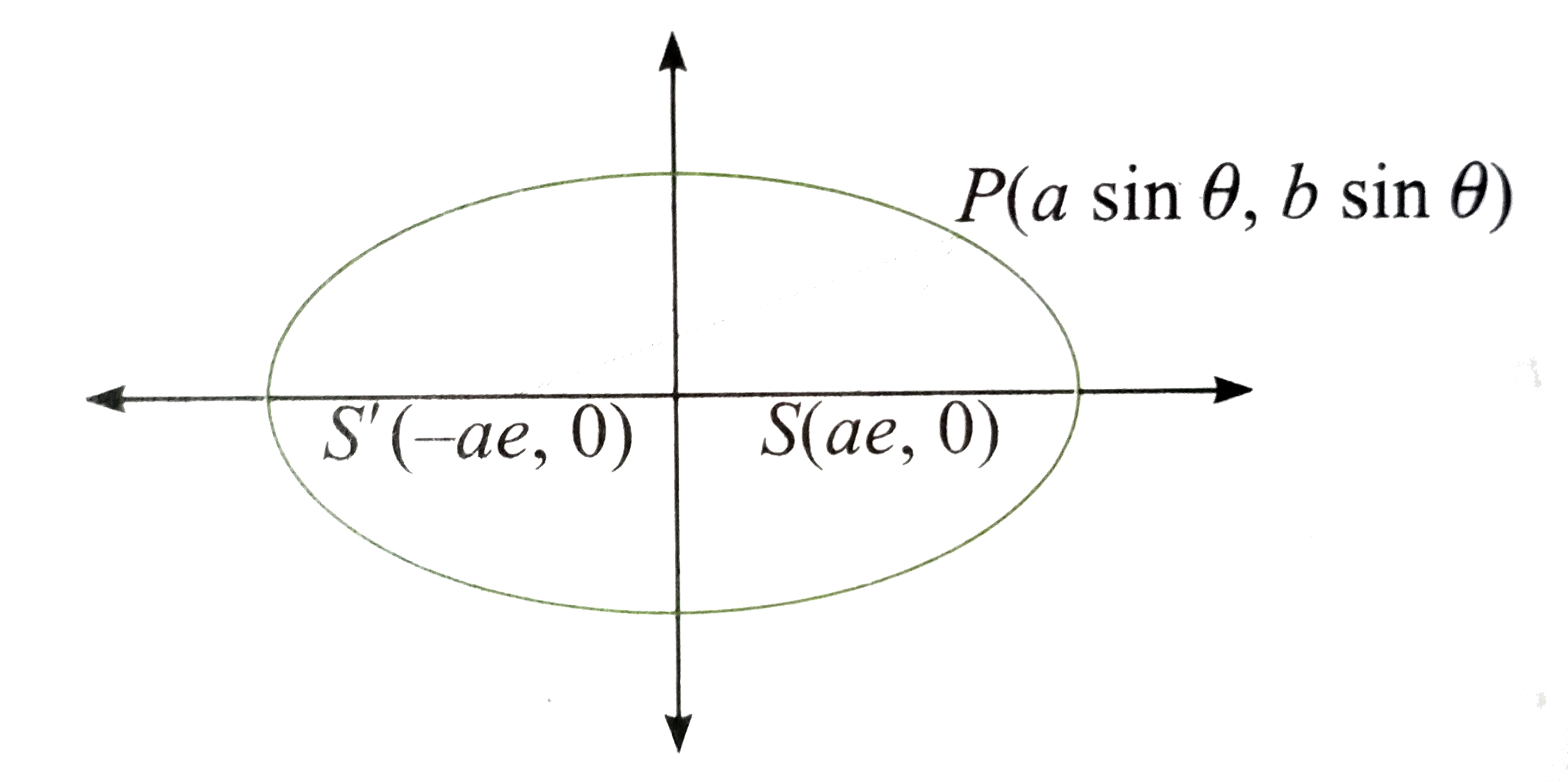
- Let S and S' be the foci of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- If P is a variable point on the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- The normal at a variable point P on the ellipse (x^2)/(a^2)+(y^2)/(b^2...
Text Solution
|
- A variable point P on the ellipse of eccentricity e is joined to the f...
Text Solution
|
- Let S and S'' be the fociof the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2)...
Text Solution
|
- Let S and S'' be the foci of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2...
Text Solution
|
- Let the foci of the ellipse (x^(2))/(9) + y^(2) = 1 subtend a right ...
Text Solution
|
- Find the equation of the ellipse whose length of major axis is 4 and l...
Text Solution
|
- Let A be point on the ellipse ((x-2)^(2))/(16)+(y^(2))/(12)=1, B and C...
Text Solution
|