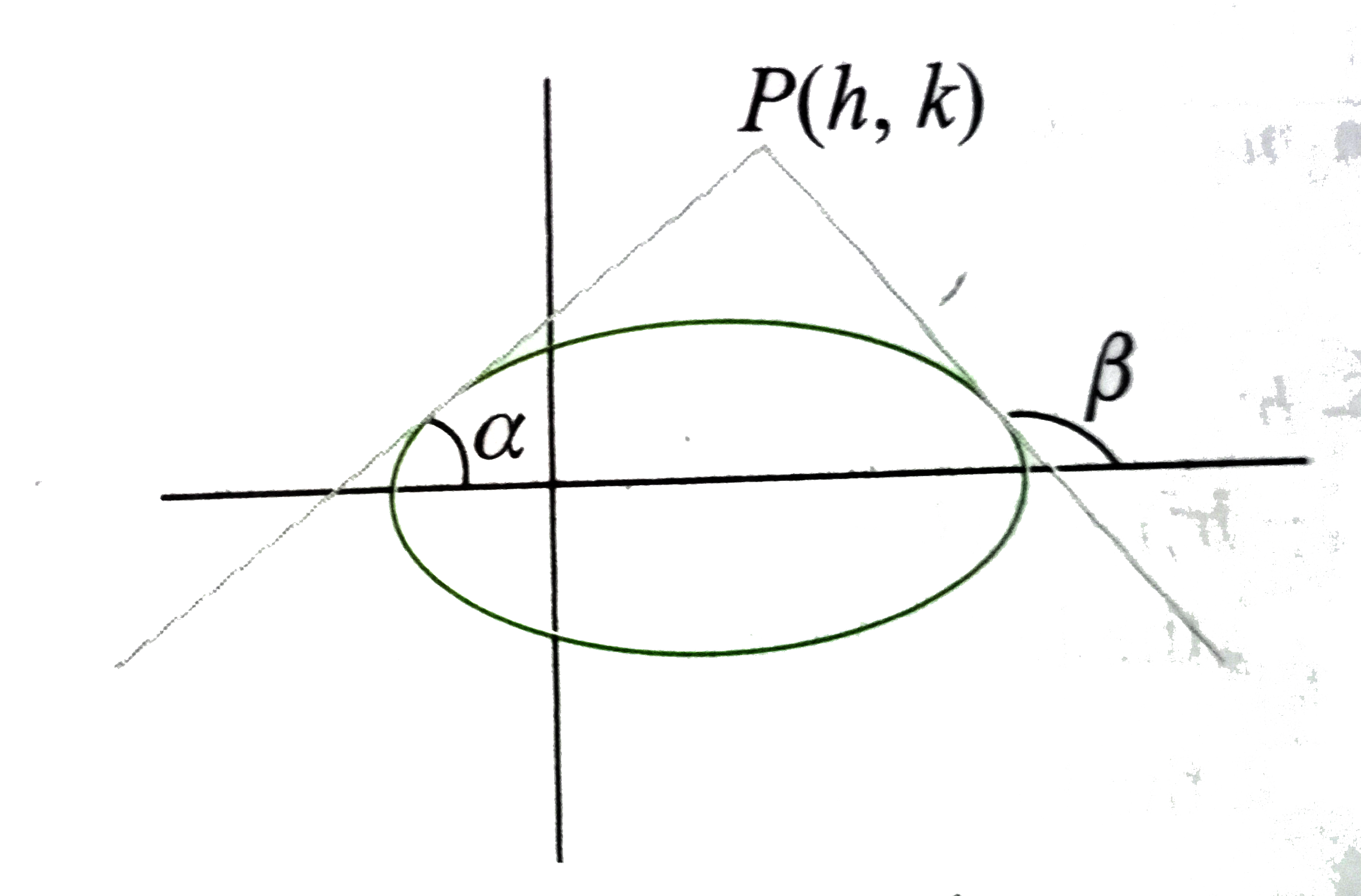Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The tangents drawn from a point P to ellipse (x^(2))/(a^(2))+(y^(2))/(...
Text Solution
|
- Tangents are drawn to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 at...
Text Solution
|
- Prove that the locus of a point,tangents from where to hyperbola x^(2)...
Text Solution
|
- Tangents drawn from the point (c, d) to the hyperbola (x^(2))/(a^(2))-...
Text Solution
|
- Two tangents are drawn from a point on hyperbola x^(2)-y^(2)=5 to the...
Text Solution
|
- If the tangents drawn from a point on the hyperbola x^(2)-y^(2)=a^(2)-...
Text Solution
|
- Tangents drawn from the point (c,d) to the hyperbola (x^(2))/(a^(2))-(...
Text Solution
|
- From any point on the hyperbola x^(2) -y^(2) =a^(2) -b^(2) two tange...
Text Solution
|
- Ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 On (alpha, beta) The tangent...
Text Solution
|