Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
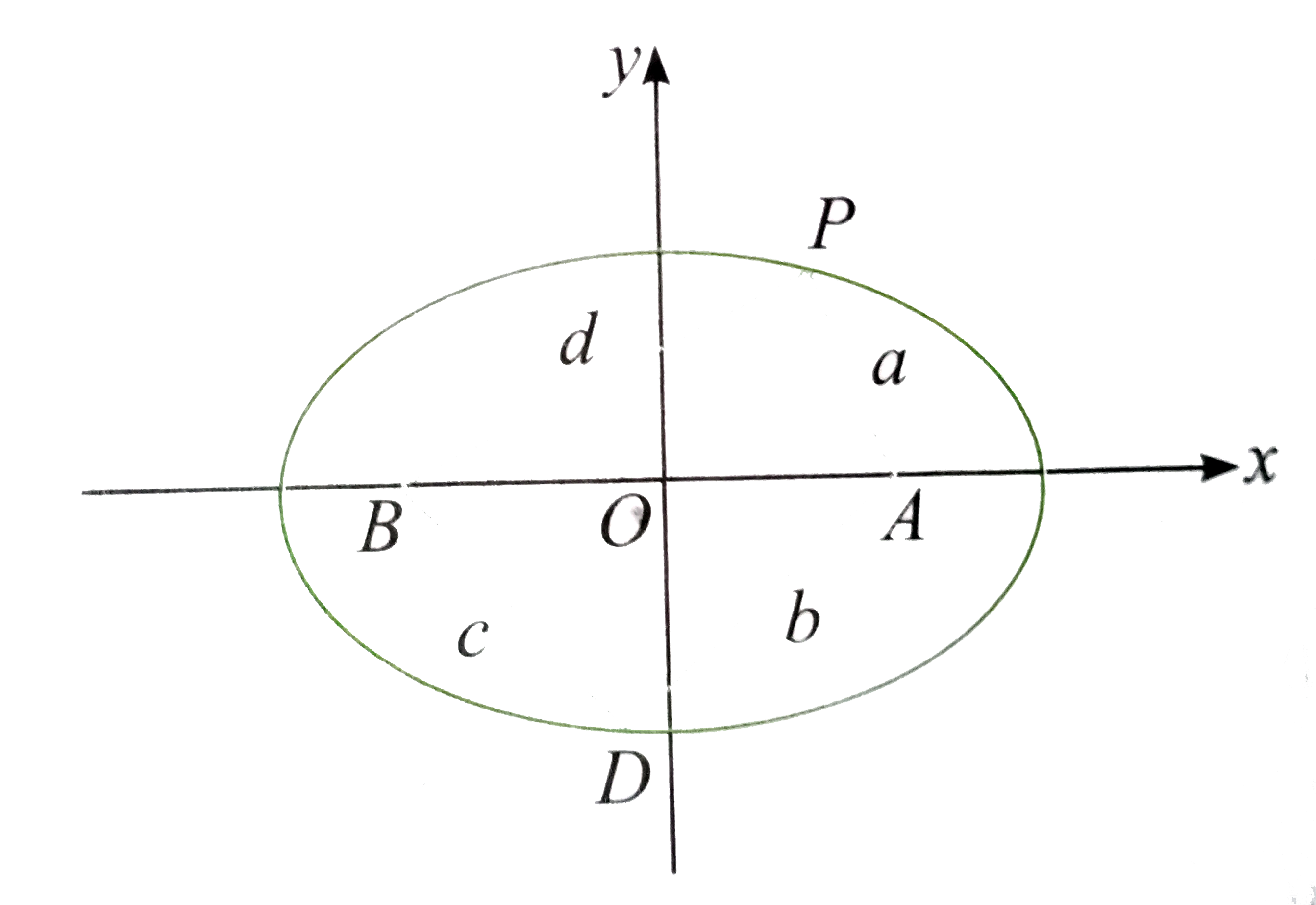
- Points P and D are taken on the ellipse (x^(2))/(4)+(y^(2))/(2)=1 . If...
Text Solution
|
- A tangent is drawn to the ellipse to cut the ellipse (x^(2))/(a^(2))+(...
Text Solution
|
- If P is any point on ellipse (x^(2))/(4)+4y^(2)=1 whose foci are at A ...
Text Solution
|
- Let the foci of the ellipse (x^(2))/(9)+y^(2)=1 subtend a right angle ...
Text Solution
|
- Points P and D are taken on the ellipse (x^(2))/(4)+(y^(2))/(2)=1 . If...
Text Solution
|
- The straight line (x)/(4)+(y)/(3)=1 intersects the ellipse (x^(2))/(16...
Text Solution
|
- Find the length of the latus rectum of the ellipse 5x^(2) + 3y^(2) = ...
Text Solution
|
- Let P be a variable point on the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 wit...
Text Solution
|
- Let d be the perpendicular distance from the centre of the ellipse x^(...
Text Solution
|