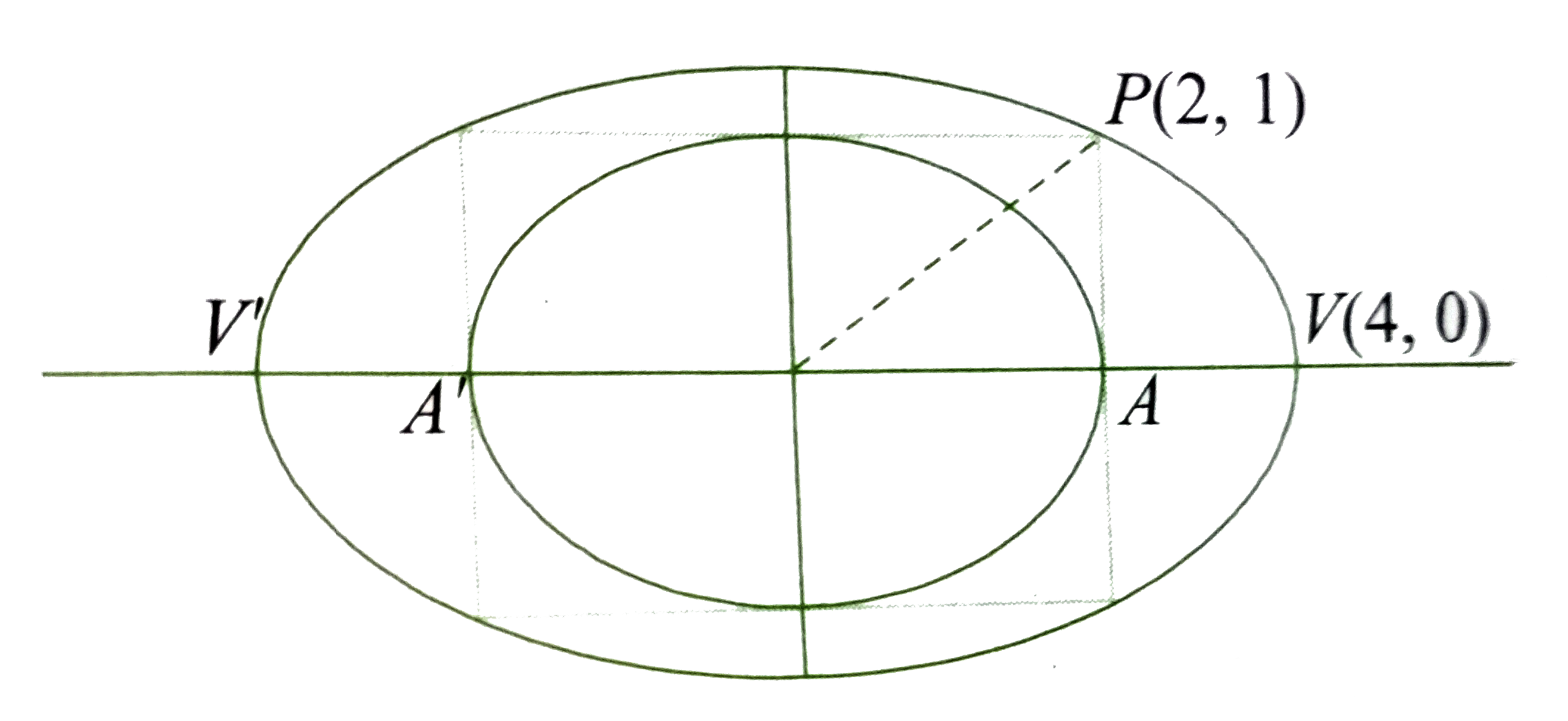
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The ellipse x^2+""4y^2=""4 is inscribed in a rectangle aligned with...
Text Solution
|
- An ellipse is drawn by taking a diameter of the circle (x)^2+""y^2=""1...
Text Solution
|
- The area of the rectangle of maximum area inscribed in the ellipse (x^...
Text Solution
|
- The area of the rectangle of maximum area inscribed in the ellipse (x^...
Text Solution
|
- Ellipse x^(2) + 4y^(2) = 4 is inscribed in a rectangle aligned with...
Text Solution
|
- The ellipse E(1):(x^(2))/(9)+(y^(2))/(4)=1 is inscribed in a rectangle...
Text Solution
|
- Area of the greatest rectangle inscribed in the ellipse (x^(2))/(16)+(...
Text Solution
|
- The product of the slopes of the common tangents of the ellipse x^(2)+...
Text Solution
|
- A common tangent to the circle x^(2) +y^(2) =16 and an ellipse (x^(2...
Text Solution
|