Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The radius of the circle passing through the foci of the ellipse (x^2)...
Text Solution
|
- the equilibrium of the circle passing through the foci of the el...
Text Solution
|
- The radius of the circle passing through the foci of (x^(2))/(16) + (y...
Text Solution
|
- वृत्त की त्रिज्या ज्ञात कीजिए, जो दीर्घवृत्त (x^(2))/(16)+(y^(2))/(9)=...
Text Solution
|
- The radius of the circle passing through the foci of the ellipse 9x^(2...
Text Solution
|
- The equation of the circle passing through the foci of the ellipse (x^...
Text Solution
|
- The equation of the circle passing through the foci of the ellipse x^(...
Text Solution
|
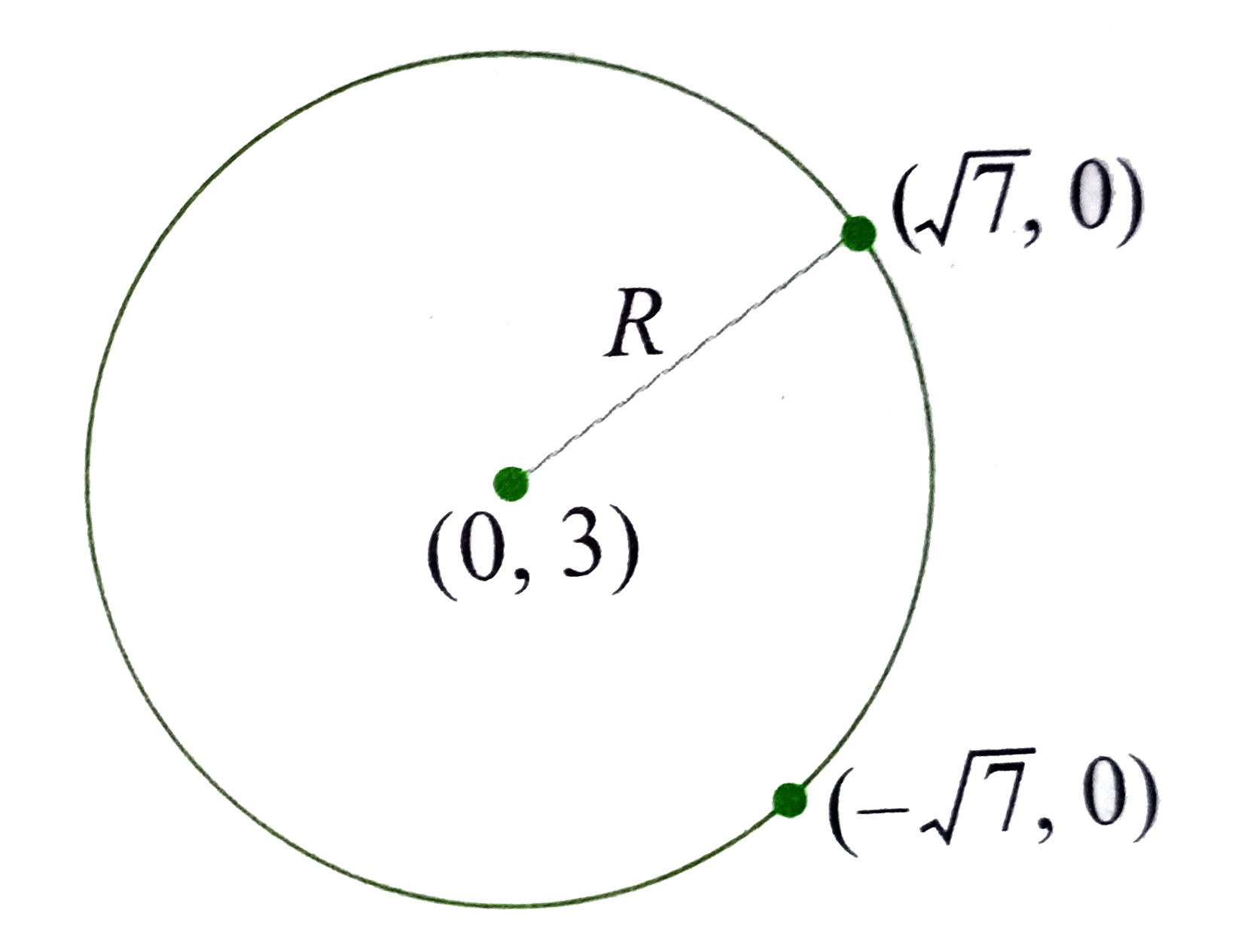
- उस वृत्त का समीकरण जिसका केन्द्र (0, 3) पर है तथा जो दीर्घवृत्त (x^(...
Text Solution
|
- The radius of the circle passing throught the foci of the ellipse x^(2...
Text Solution
|