A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
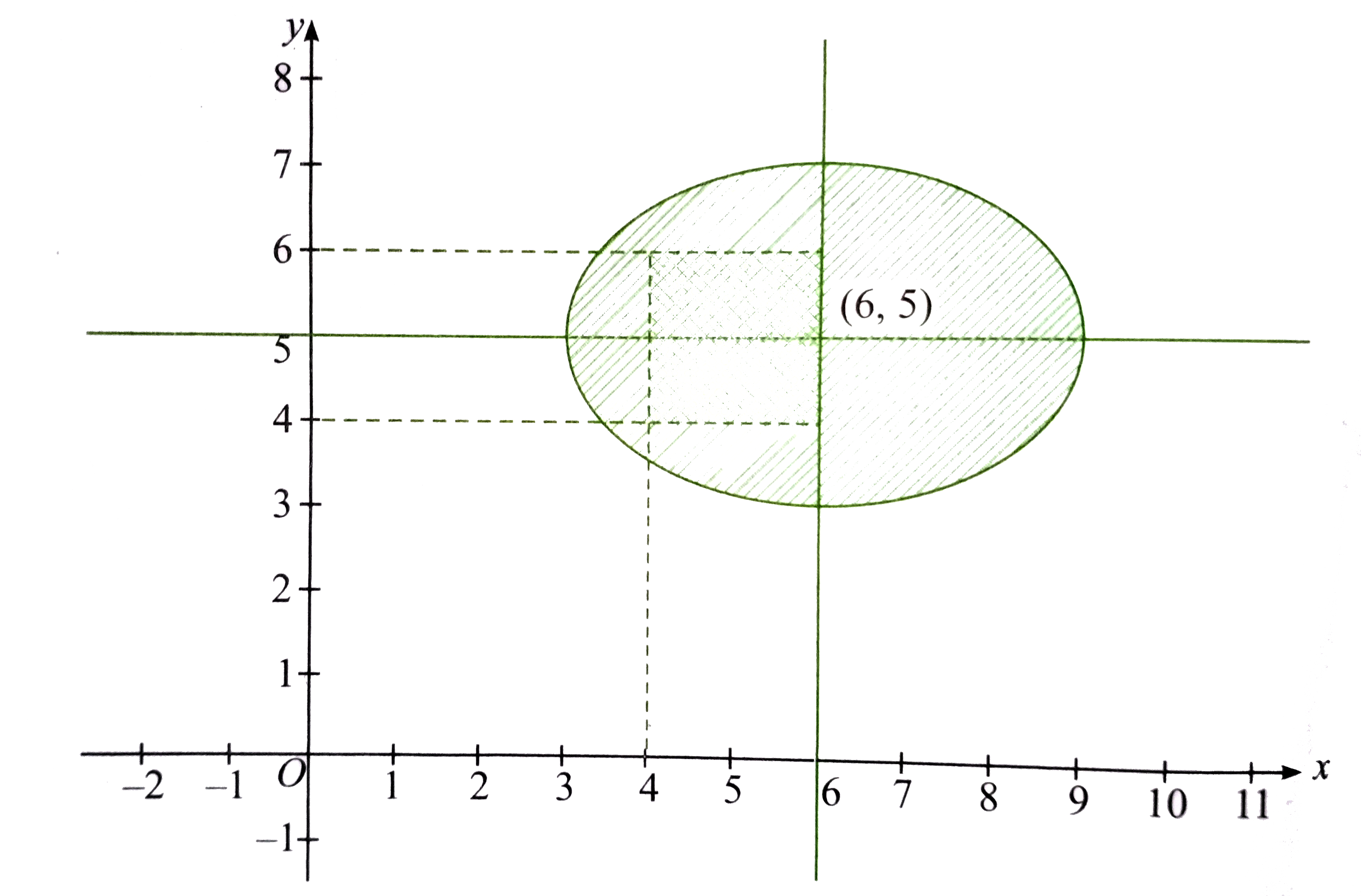
- Two sets A and B are as under A=|(a,b) in RxxR:|a-5| lt 1 and |b-5| lt...
Text Solution
|
- Let A and B be two non-empty subsets of set X. If (A-B)U(B-A)=AUB then...
Text Solution
|
- Two sets A and B are as under A=|(a,b) in RxxR:|a-5| lt 1 and |b-5| lt...
Text Solution
|
- Given two sets A and B,A sub B iff A backslash B=phi
Text Solution
|
- State whether the given statement is true or false : (i) if A sub B ...
Text Solution
|
- दो समुच्चय A तथा B इस प्रकार है कि A={(a,b) in R xx R :|a-5| lt 1 तथ...
Text Solution
|
- दो समुच्चय A तथा B इस प्रकार है कि A={a,b) in R xx R :| a-5|lt 1 ...
Text Solution
|
- Two sets A and B are as under A=|(a,b) in RxxR:|a-5| lt 1 and |b-5| lt...
Text Solution
|
- For all sets A, B and C, if A sub B And B sub C , so A cup B sub C
Text Solution
|