Home
Class 12
MATHS
If the area enclosed between f(x)=min (c...

If the area enclosed between `f(x)=min (cos ^-1(cos x).cot ^-1(cot x))` and `x` -axis in `x in(pi, 2 pi)` is `(pi^2)/k` where `k in N`, then `k` is equal to

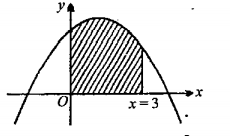
Text Solution

Verified by Experts

The correct Answer is:
4
Promotional Banner

Topper's Solved these Questions

  • AREA

    CENGAGE|Exercise Comprehension Type|2 Videos

  • BINOMIAL THEOREM

    CENGAGE|Exercise Comprehension|11 Videos

Similar Questions

Explore conceptually related problems

If the area enclosed by the curves f(x) = cos^(-1) (cos x) and g(x) = sin^(-1) (cos x) " in " x in [9 pi//4, 15 pi//4] " is " api^(2)//b (where a and b are coprime), then the value of b is ____

Find the area enclosed the curve y=sin x and the X-axis between x=0 and x=pi .

Find the area enclosed the curve y=sin x and the X-axis between x=0 and x=pi .

If 1 + cos x=k where x is acute , then sin x/2

Solve cos 2x=|sin x|, x in (-pi/2, pi) .

Solve cos 2x=|sin x|, x in (-pi/2, pi) .

If cos^(-1)x + cot^(-1) (1/2) = pi/2 then x is equal to

Find the range of f(x) = (sin^(-1) x)^(2) + 2pi cos^(-1) x + pi^(2)

The area enclosed by y=x^(2)+ cos x" and its normal at "x=(pi)/(2) in the first quadrant is

If ( sin x ) /( cos x) xx ( sec x )/( cosec x ) xx ( tan x )/( cot x) = 9 , where x in ( 0, (pi)/(2)) then the value of x is equal to