A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
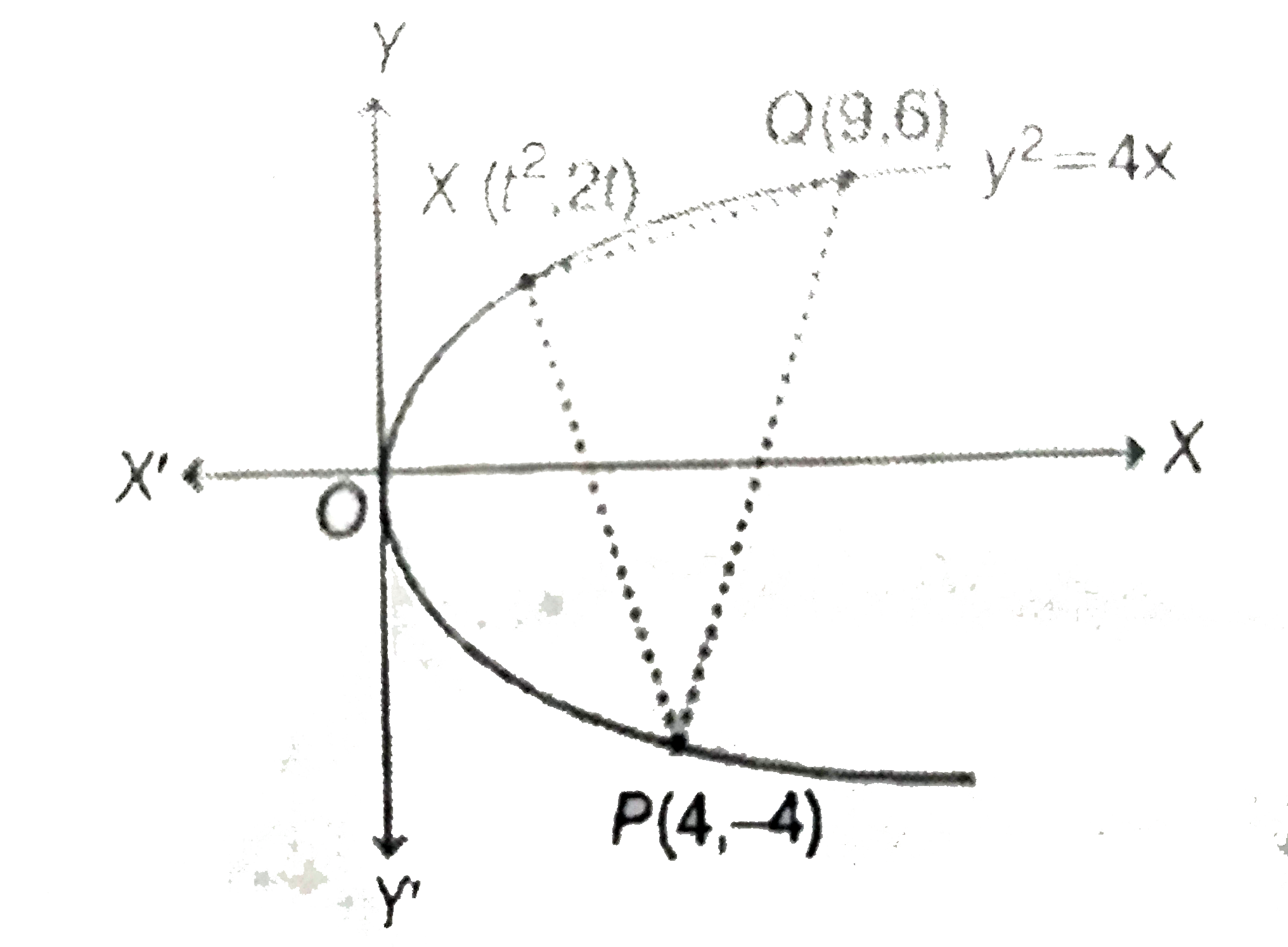
- Consider the parabola y^(2)=4x, let P and Q be two points (4,-4) and (...
Text Solution
|
- Let P,Q,R be three points on a parabola, normals at which are concurre...
Text Solution
|
- Let P(4,-4) and Q(9,6) be points on the parabola y^(2)=4a(x-b). Let R ...
Text Solution
|
- Consider the parabola y^(2)=4x, let P and Q be two points (4,-4) and (...
Text Solution
|
- Let A(4,-4) and B(9,6) be points on the parabola y^(2)=4x. Let C b...
Text Solution
|
- Consider the parabola x^(2) +4y = 0. Let P(a,b) be any fixed point ins...
Text Solution
|
- Let P(4,-4) and Q(9,6) be two points on the parabola, y^2=4x and let X...
Text Solution
|
- Consider the parabola y^(2)=4x .A=(4,-4) and B=(9,6) "be two fixed poi...
Text Solution
|
- From the point (3 0) 3- normals are drawn to the parabola y^2 = 4x. Fe...
Text Solution
|