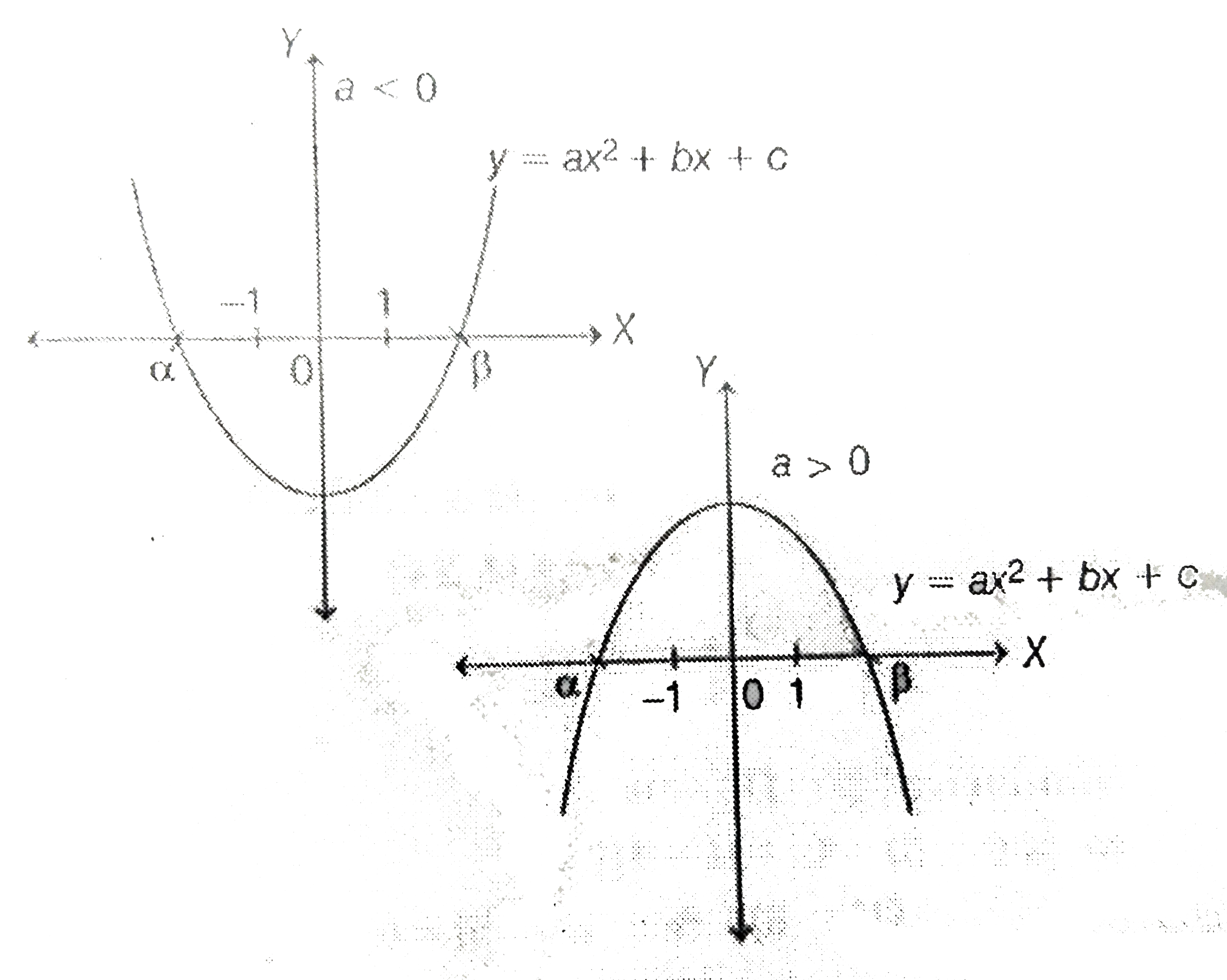Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let a ,b ,c be real. If a x^2+b x+c=0 has two real roots alphaa n dbet...
Text Solution
|
- Consider two complex numbers alphaa n dbeta as alpha=[(a+b i)//(a-b i...
Text Solution
|
- If alphaa n dbeta,alphaa n dgamma,alphaa n ddelta are the roots of th...
Text Solution
|
- Consider two complex numbers alphaa n dbeta as alpha=[(a+b i)//(a-b i)...
Text Solution
|
- If alphaa n dbeta are the roots of ax^2+bx+c=0a n dSn=alpha^n+beta^n,...
Text Solution
|
- If alphaa n dbeta,alphaa n dgamma,alphaa n ddelta are the roots of th...
Text Solution
|
- Let a ,b ,c be real. If a x^2+b x+c=0 has two real roots alphaa n dbet...
Text Solution
|
- Let a ,b ,c be real. If a x^2+b x+c=0 has two real roots alphaa n dbet...
Text Solution
|
- If alpha is a real root of the quadratic equation a x^2+b x+c=0a n dbe...
Text Solution
|