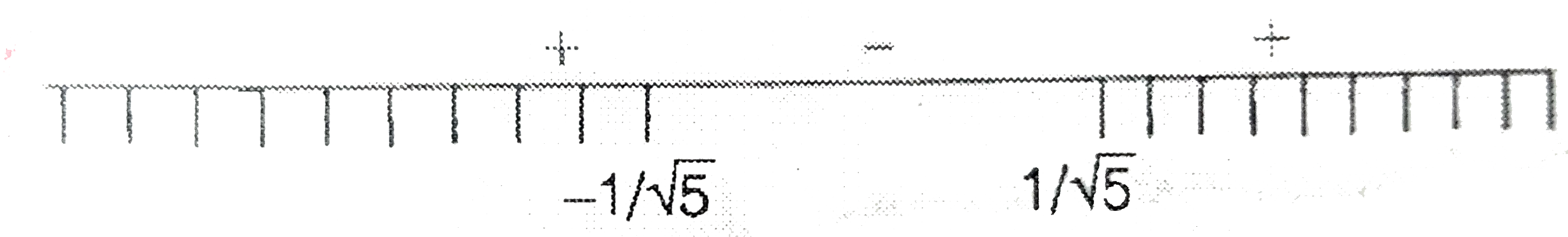A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let S be the set of all non-zero numbers alphasuch that the quadratic ...
Text Solution
|
- Let S be the set of all non-zero real numbers such that the quadratic ...
Text Solution
|
- Let S be the set of all non-zero numbers alpha such that the quadratic...
Text Solution
|
- If x1 and x2 are two distinct roots of the equation a cosx + b sinx =c...
Text Solution
|
- Let S be the set of the non zero real numbers alpha such that the quad...
Text Solution
|
- माना कि S उन सभी शून्येतर (non-zero) वास्तविक संख्याओं alpha का समुच्च...
Text Solution
|
- If x1 and x2 are the real and distinct roots of a x^2+b x+c=0, then ...
Text Solution
|
- Let S be the set of all non-zero real numbers such that the quadratic ...
Text Solution
|
- Find a quadratic equation whose product of roots x1 and x2 is equa...
Text Solution
|