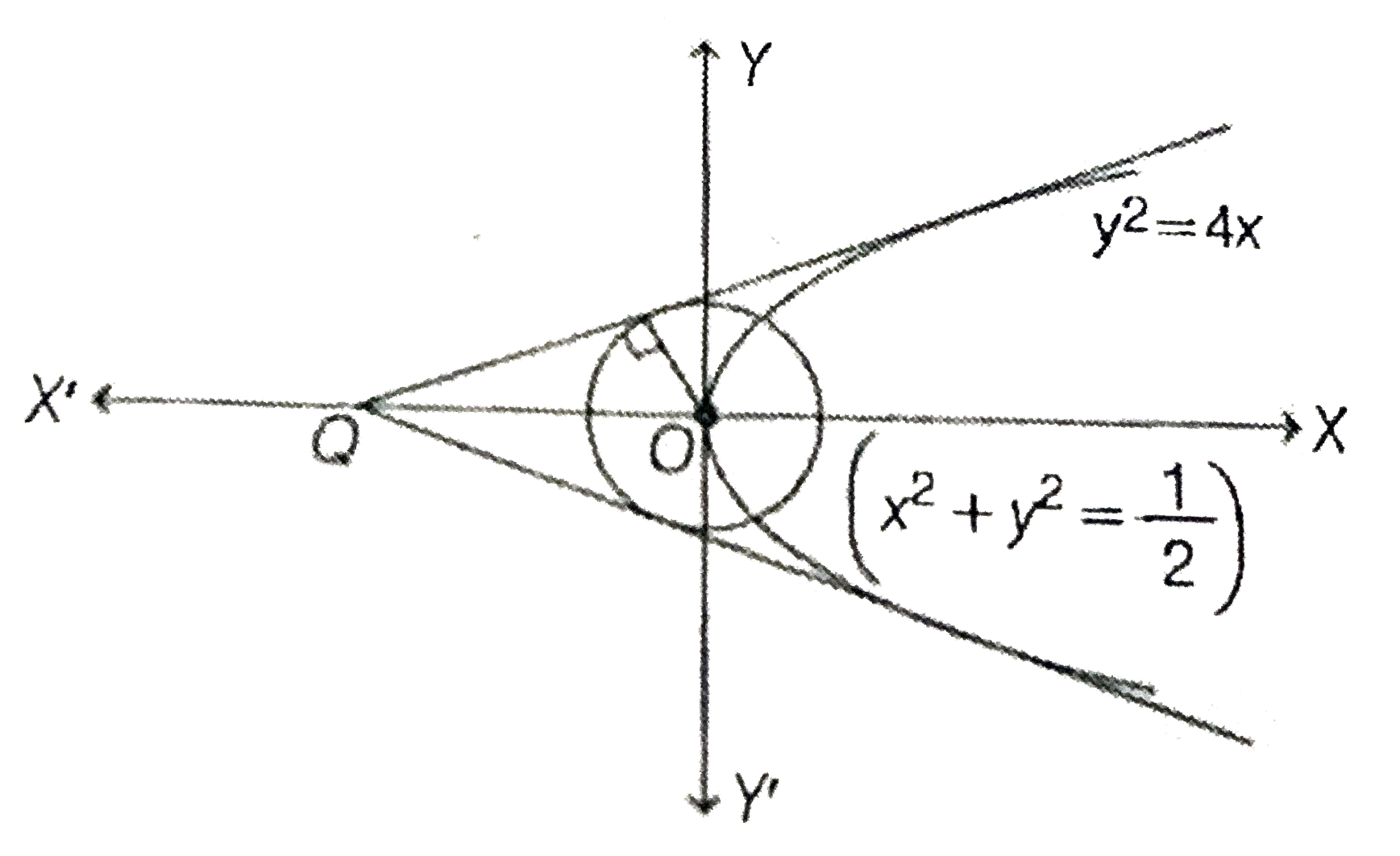
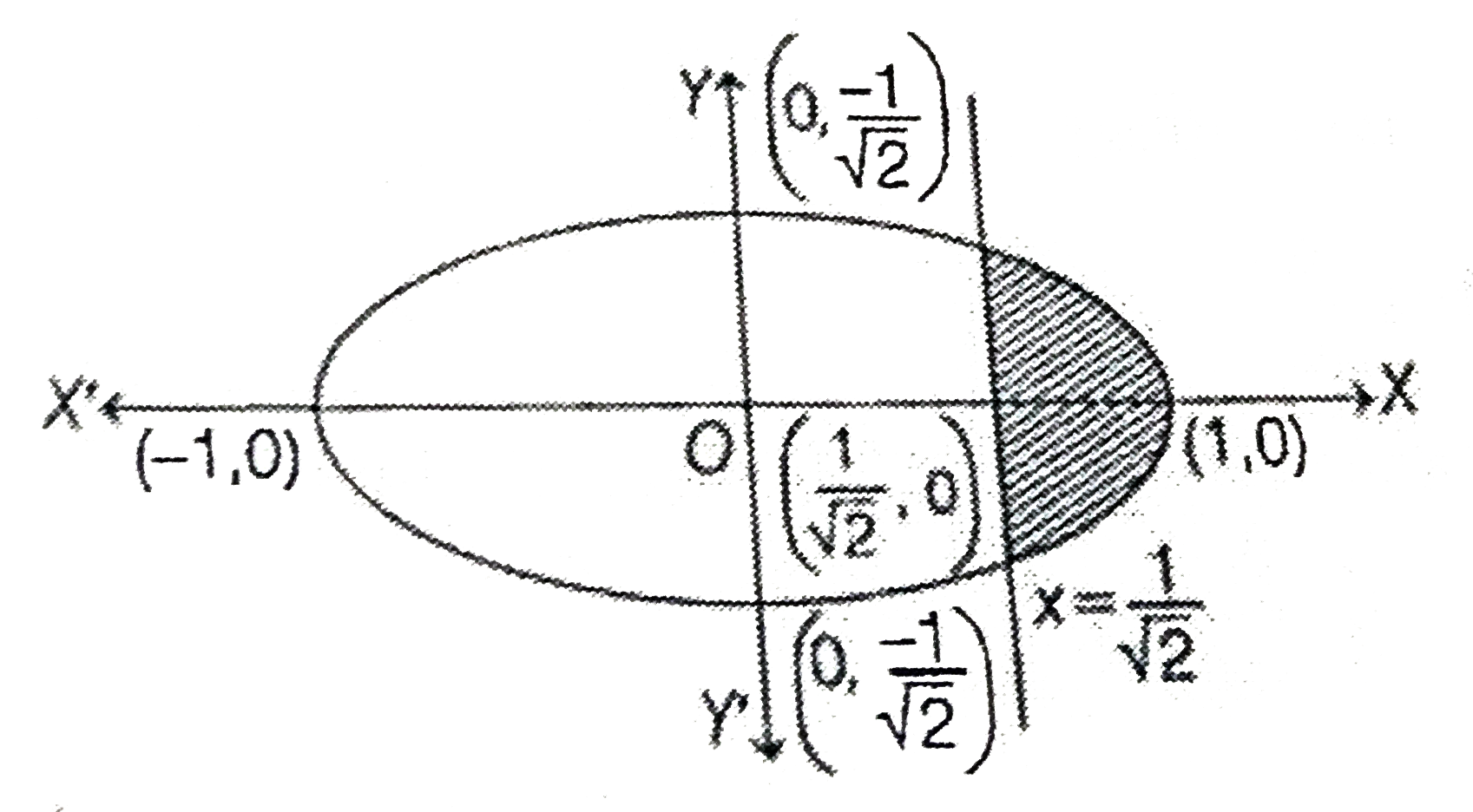
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a △ A B C , A = 30 ∘ , B = 60 and c=10. Find a and b.
Text Solution
|
- Q8) Ifa, b, c (b, care non-parallel) are unit vectors such that ax (b×...
Text Solution
|
- If an a triangle A B C ,(2cosA)/a+(cosB)/b+(2cosC)/c=a/(b c)+b/(a c), ...
Text Solution
|
- Consider the following table of inverse variation: M 1 -6 ...
Text Solution
|
- The angles A,B and C of a Delta ABC are such that A-B=15^@ and B-C=30^...
Text Solution
|
- त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए जिसमें : a= 3 , / B = 60^(@) औ...
Text Solution
|
- If, DeltaABC, B = 90^(@), C = 60^(@), b=1 find a and c
Text Solution
|
- In a triangleABC, A=30^(@), B=60^(@) . Find the other angle C
Text Solution
|
- If = 60 ^(@) , B= 30 ^(@) " then " a: b: c
Text Solution
|