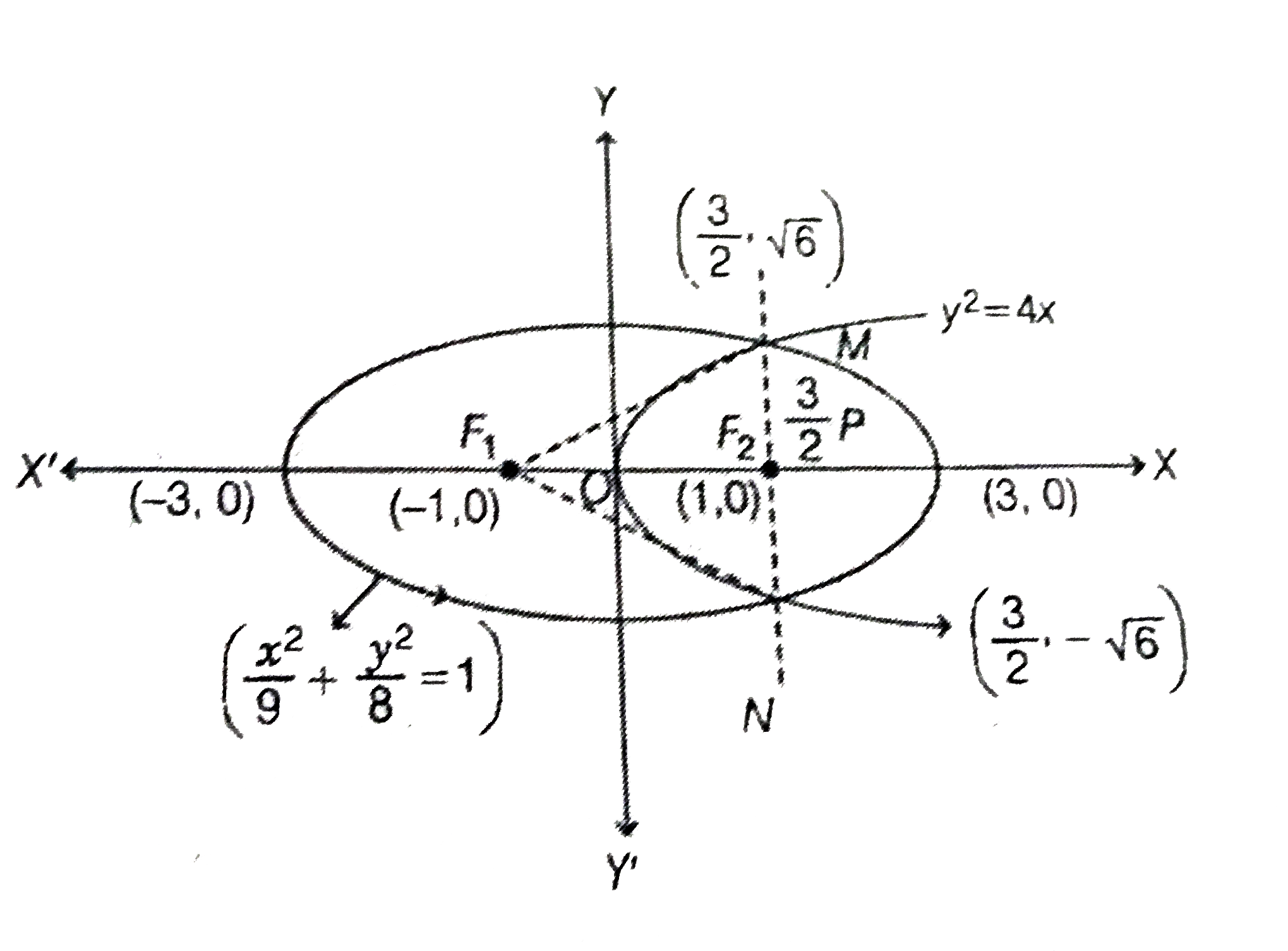
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let F(1)(x(1),0) and F(2)(x(2),0) for x(1)lt0 and x(2)gt0, be the foc...
Text Solution
|
- let A(x(1),0) and B(x(2),0) be the foci of the hyperbola (x^(2))/(9)-(...
Text Solution
|
- Let x(1) and x(2) are the roots of ax^(2)+bx+c=0 (a,b,c epsilon R) and...
Text Solution
|
- Suppose that the foci of the ellipse (x^(2))/(9)+(y^(2))/(5)=1 are (f...
Text Solution
|
- Let F(1)(x(1),0)and F(2)(x(2),0)" for "x(1)lt0 and x(2)gt0 the foci of...
Text Solution
|
- यदि X के मान x(1),x(2),x(3),……,x(n) ग्रहण करता है तथा इनके संगत बारम्ब...
Text Solution
|
- If the tangents to the ellipse at M and N meet at R and the normal to ...
Text Solution
|
- F(1) and F(2) are the two foci of the ellipse (x^(2))/(9) + (y^(2))/(4...
Text Solution
|
- Let F(1)(x(1),0) and F(2)(x(2),0), for x(1)lt0 and x(2)gt0, be the foc...
Text Solution
|