Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
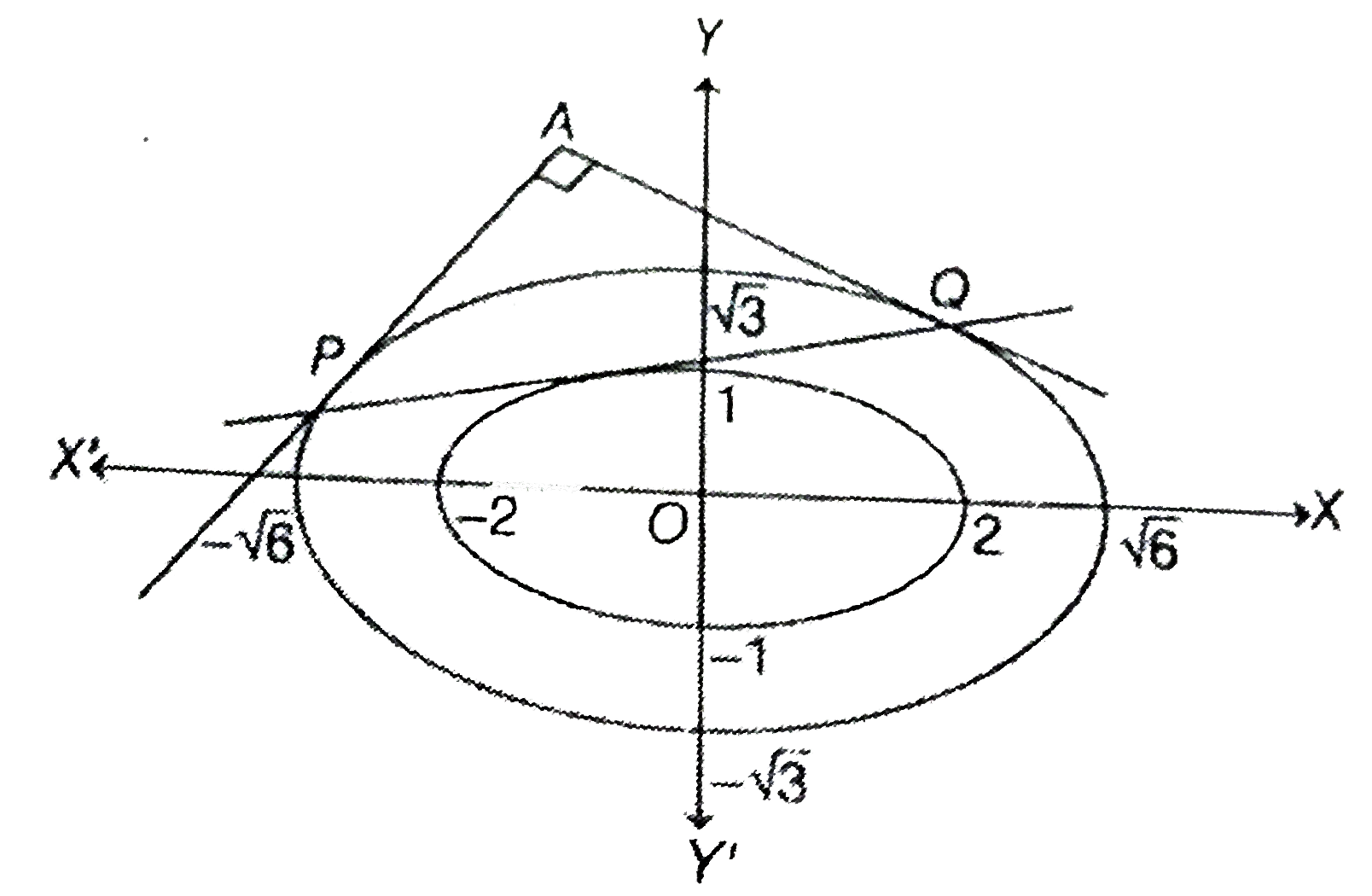
- A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 a...
Text Solution
|
- A tangent to the ellipse x^(2)+4y^(2)=4 meets the ellipse x^(2)+2y^(2)...
Text Solution
|
- The locus ofthe oot ofperpendicular rom the centre on any tangent to b...
Text Solution
|
- Tangents are drawn from a point P(6,sqrt(5)) to the ellipse (x^(2))/(2...
Text Solution
|
- Prove that the portion of the tangent to an ellipse intercepted betwee...
Text Solution
|
- A tangent to the ellipse distance distance from the centre of...
Text Solution
|
- The pole of the line y = x + 2 with respect to the ellipse x2+2y2−4x+...
Text Solution
|
- Q is a point on the auxiliary circle of an ellipse. P is the correspon...
Text Solution
|
- P & Q are the corresponding points on a standard ellipse & its auxilia...
Text Solution
|