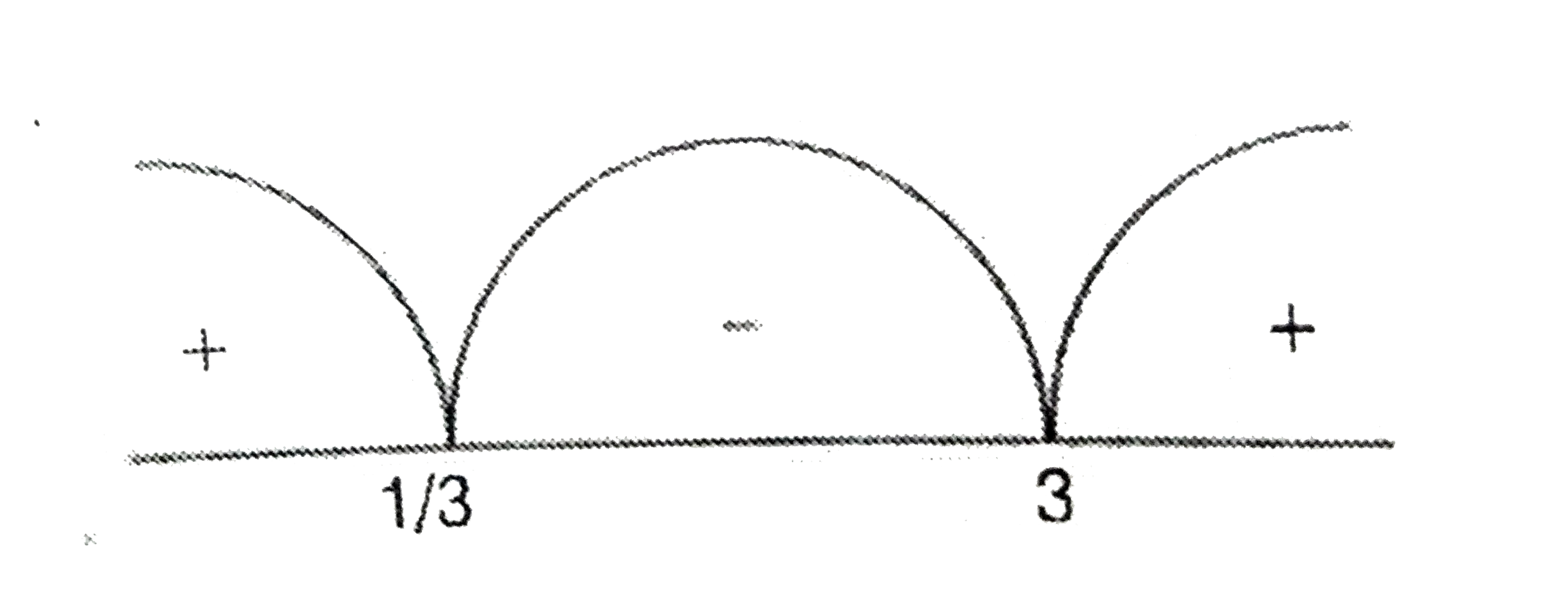
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Prove that the values of the function (sinxcos3x)/(sin3xcosx) cannot l...
Text Solution
|
- If x is real,prove that ((x-2)(x-4))/((x-1)(x-3)) can have any real va...
Text Solution
|
- If x is real,prove that ((x-2)(x-4))/((x-1)(x-3)) can have any real va...
Text Solution
|
- Prove that if the equation x^2+9y^2-4x+3=0 is satisfied for real value...
Text Solution
|
- fx be real,prove that the value of (2x^(2)-2x+4)/(x^(2)-4x+3) cannot l...
Text Solution
|
- 9Prove that the values of the function (sin x cos3x)/(sin3x cos x) can...
Text Solution
|
- The function f(x)=x^(2)+(a)/(x) cannot have a maximum at x=-3 for any ...
Text Solution
|
- 11x?+12x+6 For real values of x ,prove that x^(2)+4x+2cannot lie betwe...
Text Solution
|
- If x be real , show that the value of (2x^2-2x+4)/(x^2-4x+3) cannot li...
Text Solution
|