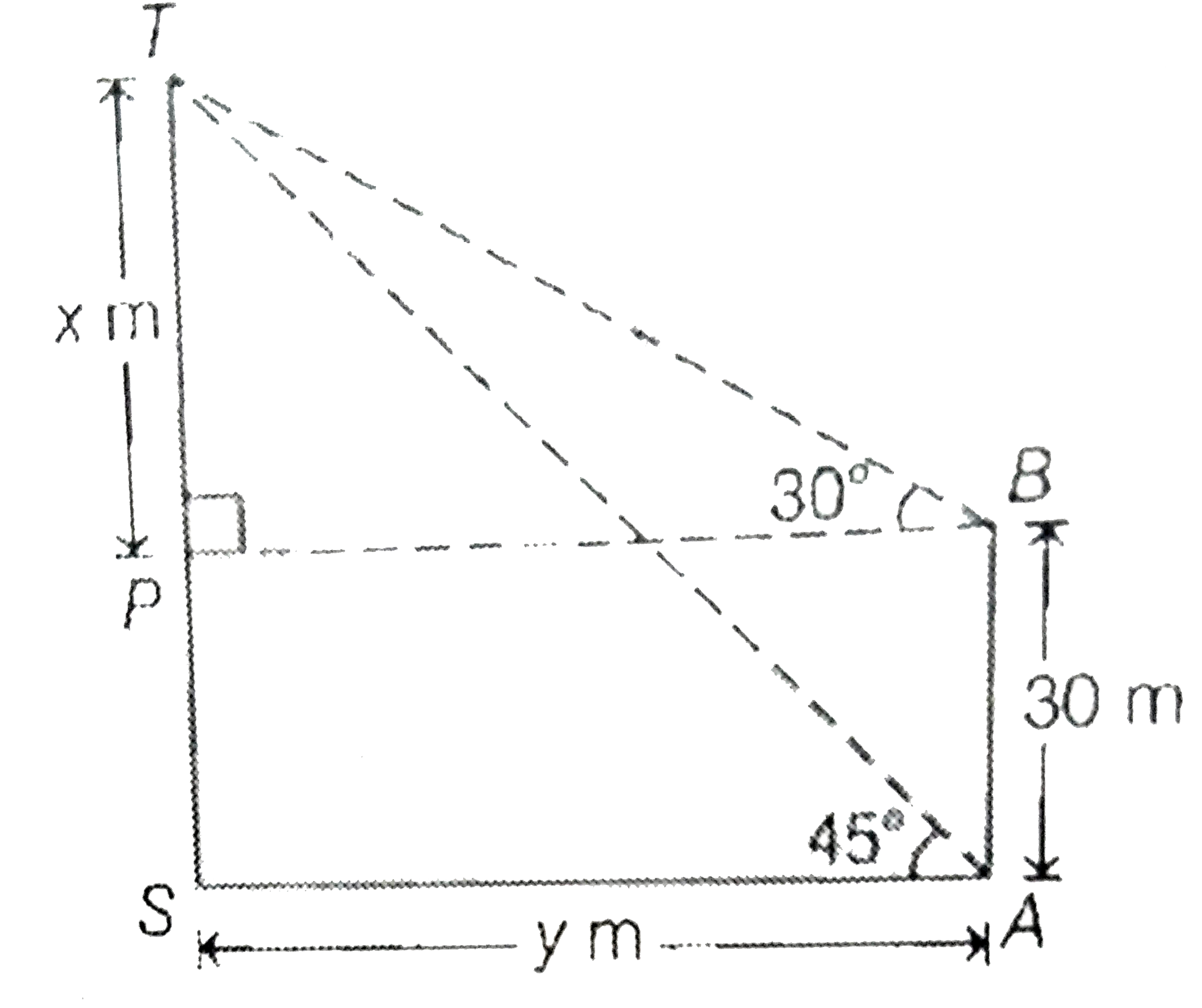
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The angle of elevation of the top of a vertical tower standing on a ho...
Text Solution
|
- Then angle of elevation of a top of tower (point B) from a point A on ...
Text Solution
|
- The angle of elevation of the loop of a vertical tower standing on a h...
Text Solution
|
- From a point on the ground 40 m away from the foot of a tower, the an...
Text Solution
|
- A tower of height 15 m stands vertically on the ground. From a point ...
Text Solution
|
- क्षैतिज तल पर खण्डी एक ऊर्ध्वाधर मीनार के शिखर का तल पर एक बिन्दु A से...
Text Solution
|
- From a point 20 m away from the foot of a tower, the angle of elevatio...
Text Solution
|
- क्षैतिज तल पर खड़ी एक ऊर्ध्वाधर मीनार के शिखर का तल पर एक बिंदु A से उन...
Text Solution
|
- A vertical tower stands on a horizontal plane, and from a point on the...
Text Solution
|