Home
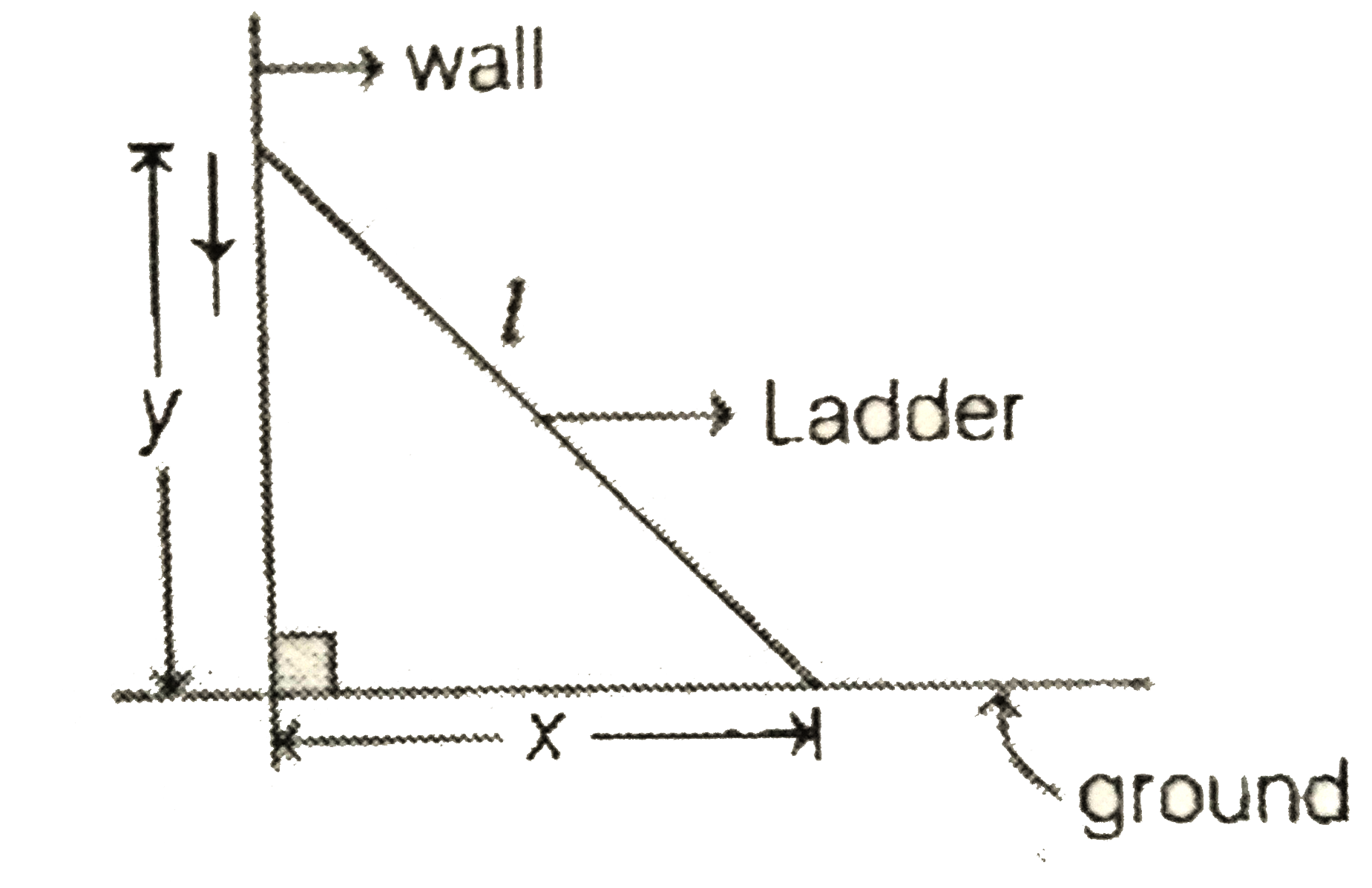
Class 12
MATHS
A 2 m ladder leans against a vertical wa...

A 2 m ladder leans against a vertical wall. If the top of the ladder begins to slide down the wall at the rate 25 cm/s, then the rate (in cm/s) at which the bottom of the ladder slides away from the wall on the horizontal ground when the top of the ladder is 1 m above the ground is

A

`25sqrt(3)`

B

`(25)/(sqrt(3))`

C

`(25)/(3)`

D

25

Text Solution

Verified by Experts

The correct Answer is:
B
Given a lader of length l = 2m leans against a vertical wall. Now, the top of ladder begins to slide down the wall at the rate 25 cm/s.
Let the rate at which bottom of the ladder slides away from the wall on the horizontal ground is `(dx)/(dt) cm//s`.

`because x^(2)+y^(2)=l^(2) " [by Pythagoras theorem]"`
`implies x^(2)+y^(2)=4 " "[becausel=2m]...(i)`
On differentiating both slides of Eq. (i) w.r.t. 't' we get
`2x(dx)/(dt)+2y(dy)/(dt)=0`
`implies (dx)/(dt)=-((y)/(x))(dy)/(dt)" ...(ii)"`
From Eq. (i), when y = 1m, then
`x^(2)+1^(2)=4impliesx^(2)=3impliesx=sqrt(3)m " "[because "x " gt 0]`
On substituting x = `sqrt(3)m` and y = 1m in Eq. (ii), we get
`(dx)/(dt)=-(1)/(sqrt(3))(-(25)/(100))m//s" "["given " (dy)/(dt)=-25cm//sec]`
`=(25)/(sqrt(3))cm//s`
Promotional Banner

Similar Questions

Explore conceptually related problems

A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?

A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5m/s. When the base of the ladder is 8 metres from the wall. How fast is the top of the ladder moving down the wall?

A ladder makes an angle of 60° with the ground, when placed against a wall. If the foot of the ladder is 2m away from the wall, then the length of the ladder (in metres) is

A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5m/s. When the base of the ladder is 8 metres from the wall. At what rate, the area of the triangle formed by the ladder, wall, and the floor, is changing?

A ladder makes an angles 30^(@) with the floor and its lower end is 12m away from the wall. Find the length of the ladder.

5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.

A ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.