A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
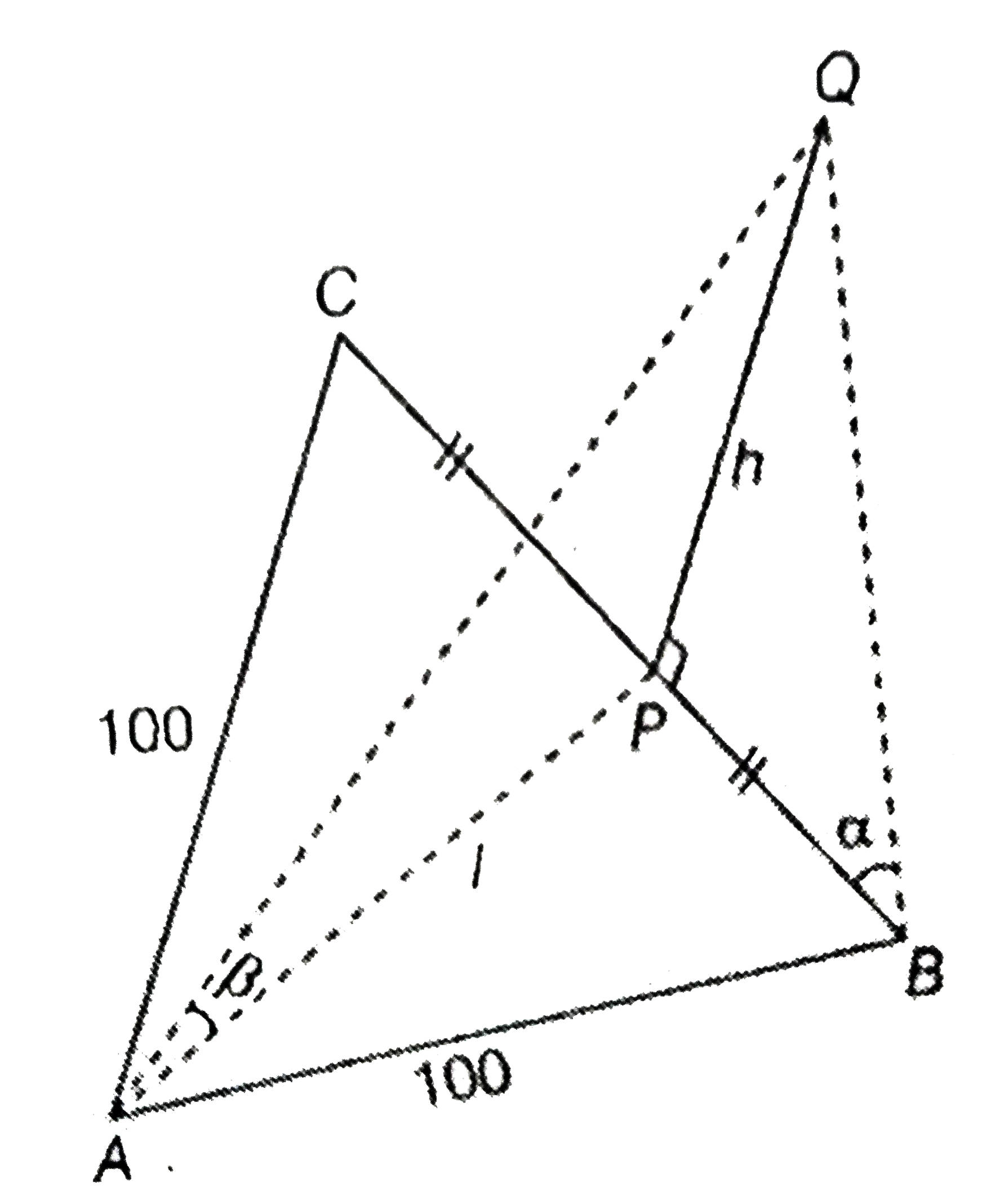
- ABC is a triangular park with AB = AC = 100 m. A vertical tower is sit...
Text Solution
|
- ABC is a triangular park with AB = AC = 100 m. A block tower is situat...
Text Solution
|
- ABC is a triangular park with AB = AC = 100 m. A block tower is situat...
Text Solution
|
- ABC is a triangular park with AB = AC = 100m. A Television tower stand...
Text Solution
|
- There are three points A, B and C horizontal plane, such that AB=AC=10...
Text Solution
|
- ABC is a triangular park with AB = AC = 100 metres. A vertical tower ...
Text Solution
|
- ABC is a triangular park with AB = AC = 100 m. A vertical tower is sit...
Text Solution
|
- ABC is a triangular park with AB=AC=100 meters. A clock tower is situa...
Text Solution
|
- ABC एक त्रिभुजाकार पार्क है, जहाँ AB=AC=100 मी | एक दूरदर्शन टॉबर (t...
Text Solution
|