A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
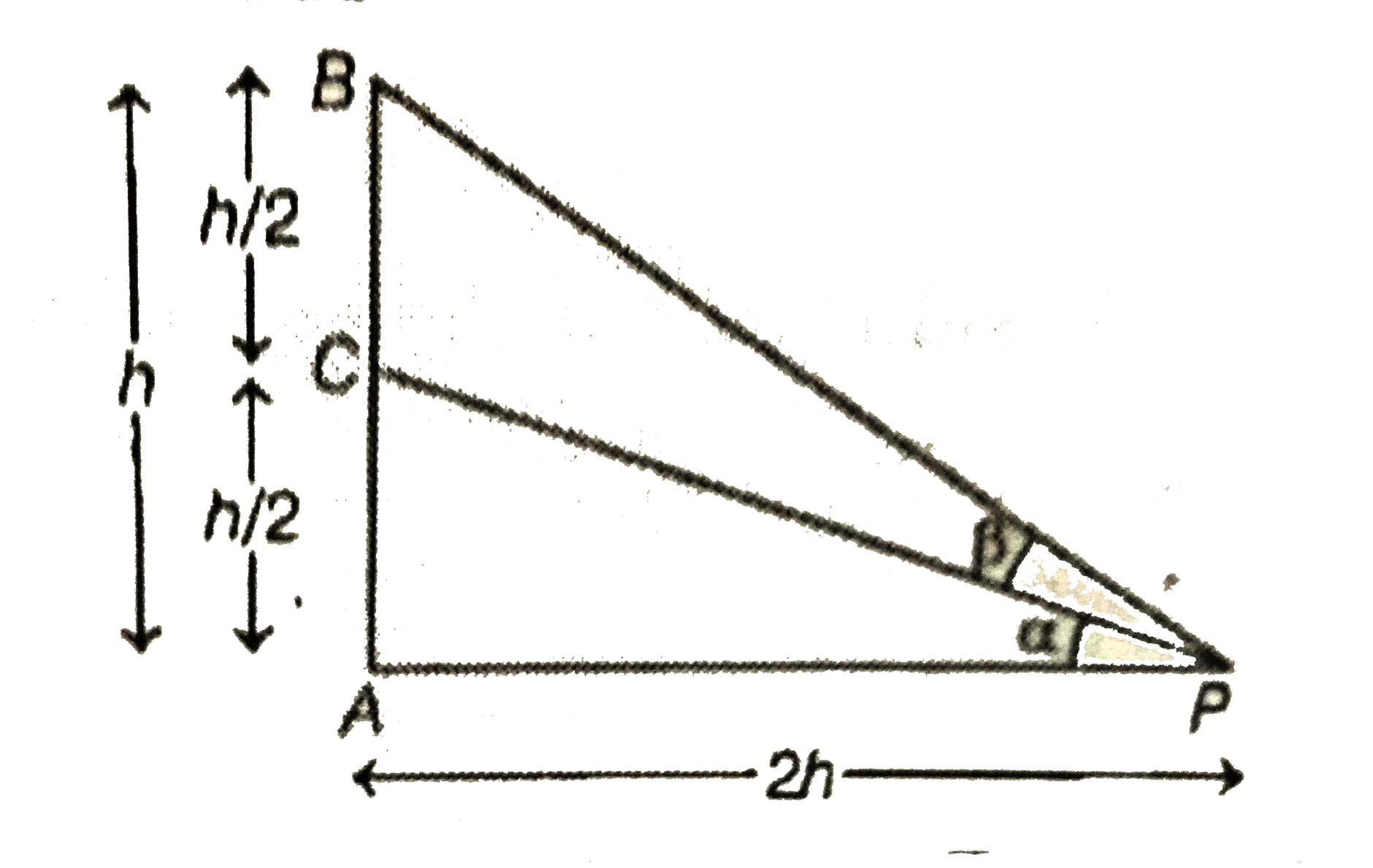
- Let a vertical tower AB have its end A on the level ground. Let C be t...
Text Solution
|
- Let a vertical tower A b have its end A on the level ground. Let C be ...
Text Solution
|
- Let a vertical tower AB have its end A on the level ground. Let C be t...
Text Solution
|
- AB is a vertical pole resting at the end A on the level ground. P is ...
Text Solution
|
- Let a vertical tower AB have its end A on the level ground. Let C be t...
Text Solution
|
- AB is a vertical pole. The end A is on the level ground .C is the midd...
Text Solution
|
- AB is a vertical pole and C is its mid point. The end A is on the leve...
Text Solution
|
- মনে করো, AB একটি টাওয়ার যার A প্রান্তটি ভূমির ওপর অবস্থিত। মনে করো, C,...
Text Solution
|
- माना एक ऊर्ध्वाधर मीनार AB ऐसी हैं कि उसका सिरा A भूमि पर हैं। म...
Text Solution
|