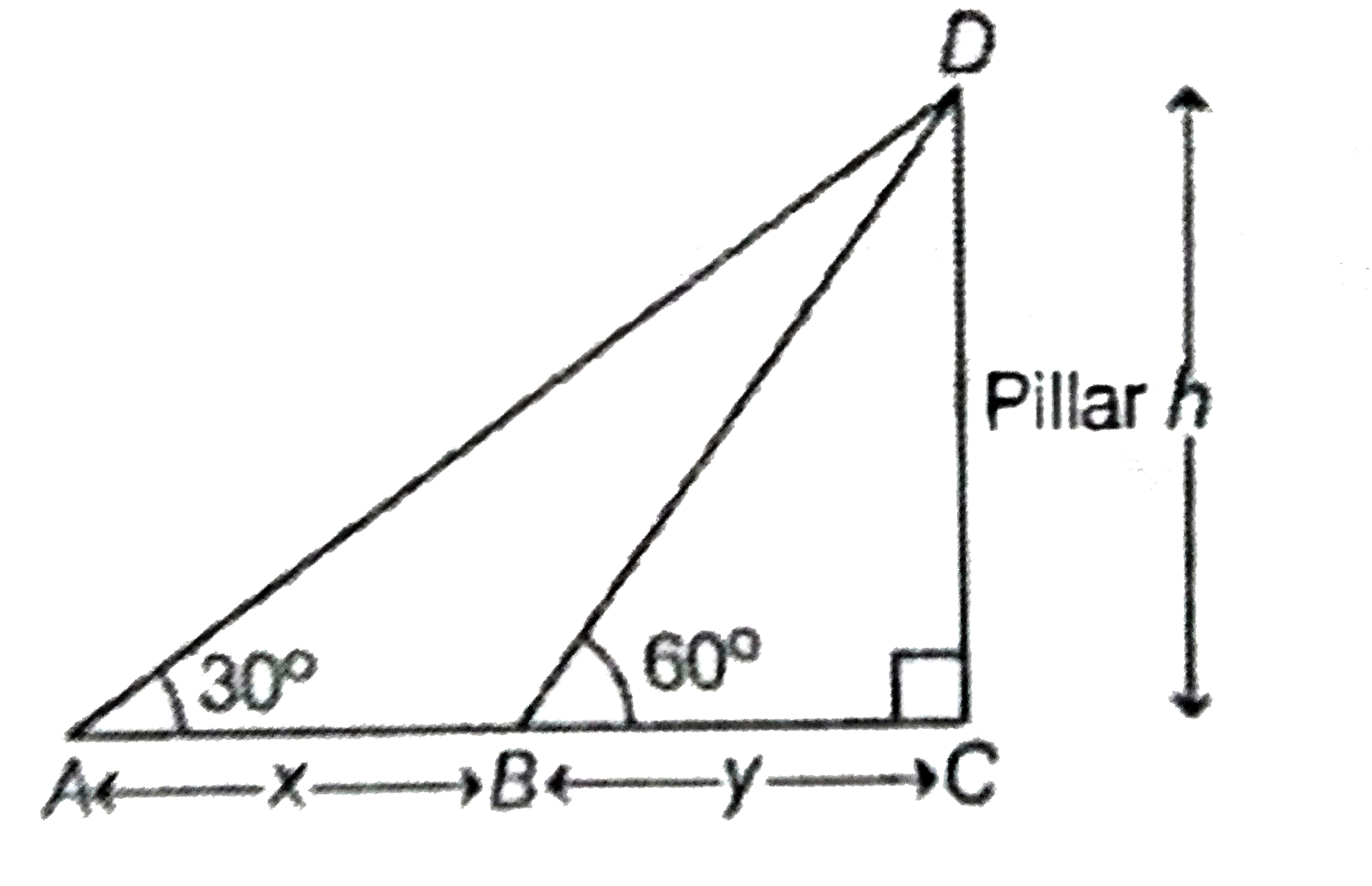
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A man is walking towards a vertical pillar in a straight path, at a ...
Text Solution
|
- A man is walking towards a vertical pillar in a straight path, at a ...
Text Solution
|
- The angle of elevation of the top of an incomplete vertical pillar at ...
Text Solution
|
- A person standing on the ground observes the angle of elevation of the...
Text Solution
|
- The angle of elevation of the top of a pillar of height h at a point o...
Text Solution
|
- एक व्यक्ति सीधे पथ पर नियत चाल से एक ऊर्ध्वाधर खम्भे की ओर जा रहा ...
Text Solution
|
- The angle of elevation of the top of an incomplete vertical pillar at ...
Text Solution
|
- एक व्यक्ति एक ऊर्ध्वाधर खम्भे की ओर एक सीधे पथ पर एकसमान चाल से जा रहा...
Text Solution
|
- A man is walking towards a vertical pillar in a straight path at a uni...
Text Solution
|