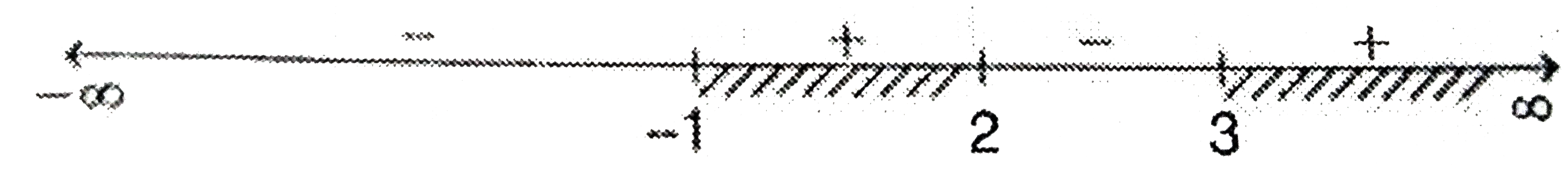Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let sqrt(((x+1)(x-3))/((x-2))). Find all the real values of x for whic...
Text Solution
|
- Let f(x)=sqrt(log(10)x^(2)) then the set of all values of x for which ...
Text Solution
|
- If x is real then (x^(2)-x+c)/(x^(2)+x+2c) can take all real values if
Text Solution
|
- Let f be a real valued function such that f(x)+3xf(1/x)=2(x+1) for all...
Text Solution
|
- Find the values of 'a' for which -3<(x^2+ax-2)/(x^2+x+1)<2 is valid fo...
Text Solution
|
- Let f(x) = sqrt(log(10)x^(2)).Find the set of all values of x for whi...
Text Solution
|
- The set of all real values of x for which the funciton f(x) = sqrt(sin...
Text Solution
|
- The real values of a for which y=sqrt(((x+1)(x-3))/(x-2)) tak...
Text Solution
|
- If (x^(2)+ax+3)/(x^(2)+x+a), takes all real values for possible real v...
Text Solution
|