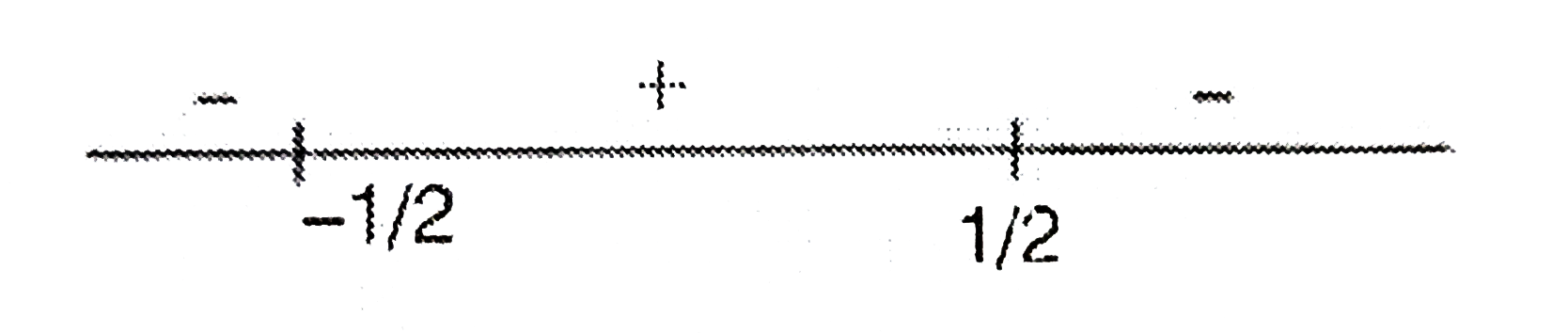
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let f: R to R be defined by f(x)=(x)/(1+x^(2)), x in R. Then, the ra...
Text Solution
|
- A function f is defined by f(x)=1/(2^(r-1)),1/(2^r)ltxlt=1 (2^(r-1)),...
Text Solution
|
- If range of y=x/(1+x^2),AAxepsilonR is equal to (A) [-1,1] ...
Text Solution
|
- Let f: R to R be defined by f(x)=(x)/(1+x^(2)), x in R. Then, the ra...
Text Solution
|
- माना A = R - {2} और B = R - {1} . यदि f : A to B , जो f (x) = (x - 1)/...
Text Solution
|
- Let f : R → R be a function defined by f ( x ) = 2 x − 5 ∀ x ∈ R . ...
Text Solution
|
- If f : R - (-1,1) to R is defined by f(x) = (x)/(x^(2)-1), verify whet...
Text Solution
|
- If f : R to R is defined by f (x) = {:{((x+2)/(x^(2)+3x+2), if x...
Text Solution
|
- माना f : R rarr R, f(x) = (x)/(1 + x^(2)), x in R द्वारा परिभाषित किया...
Text Solution
|