Home
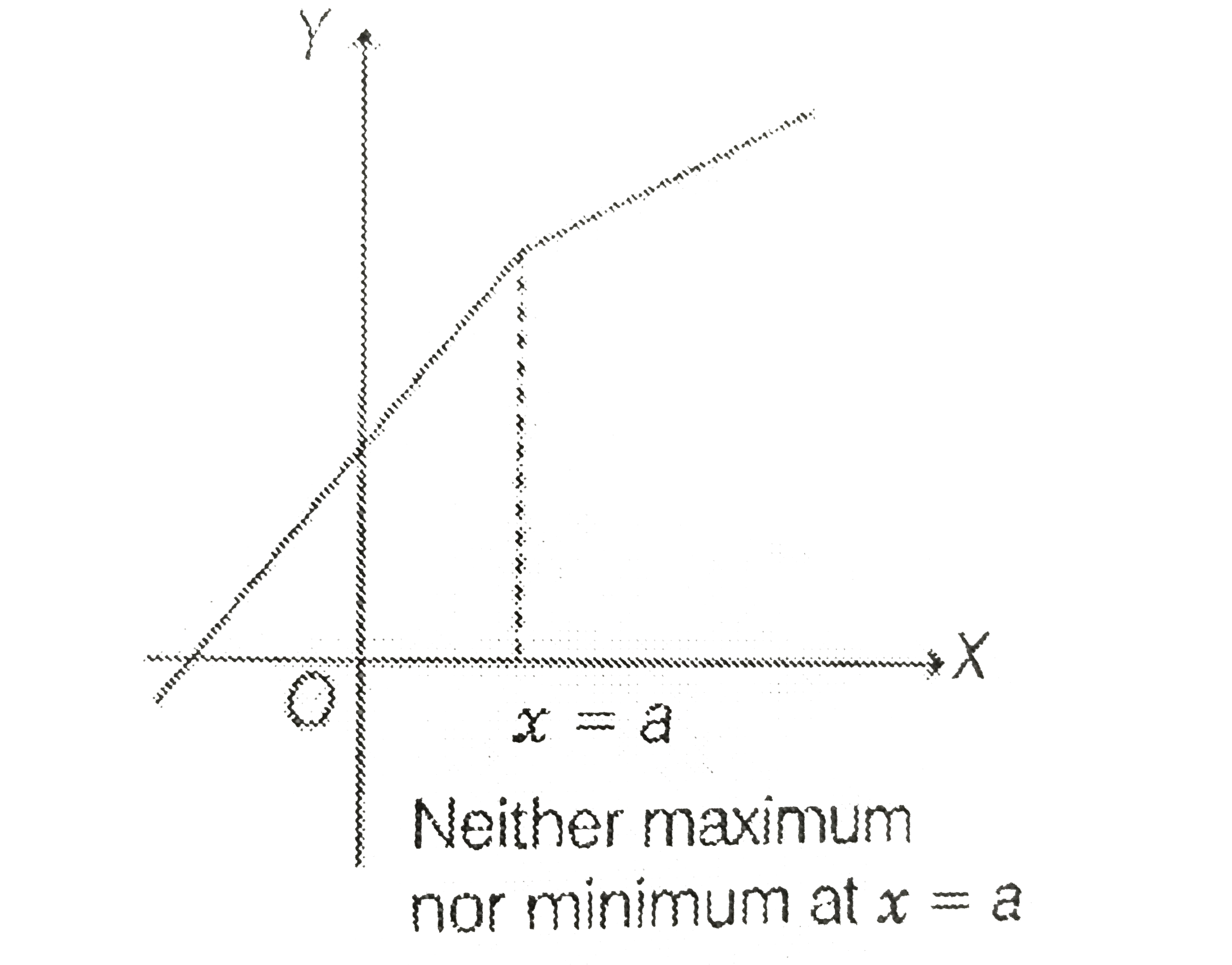
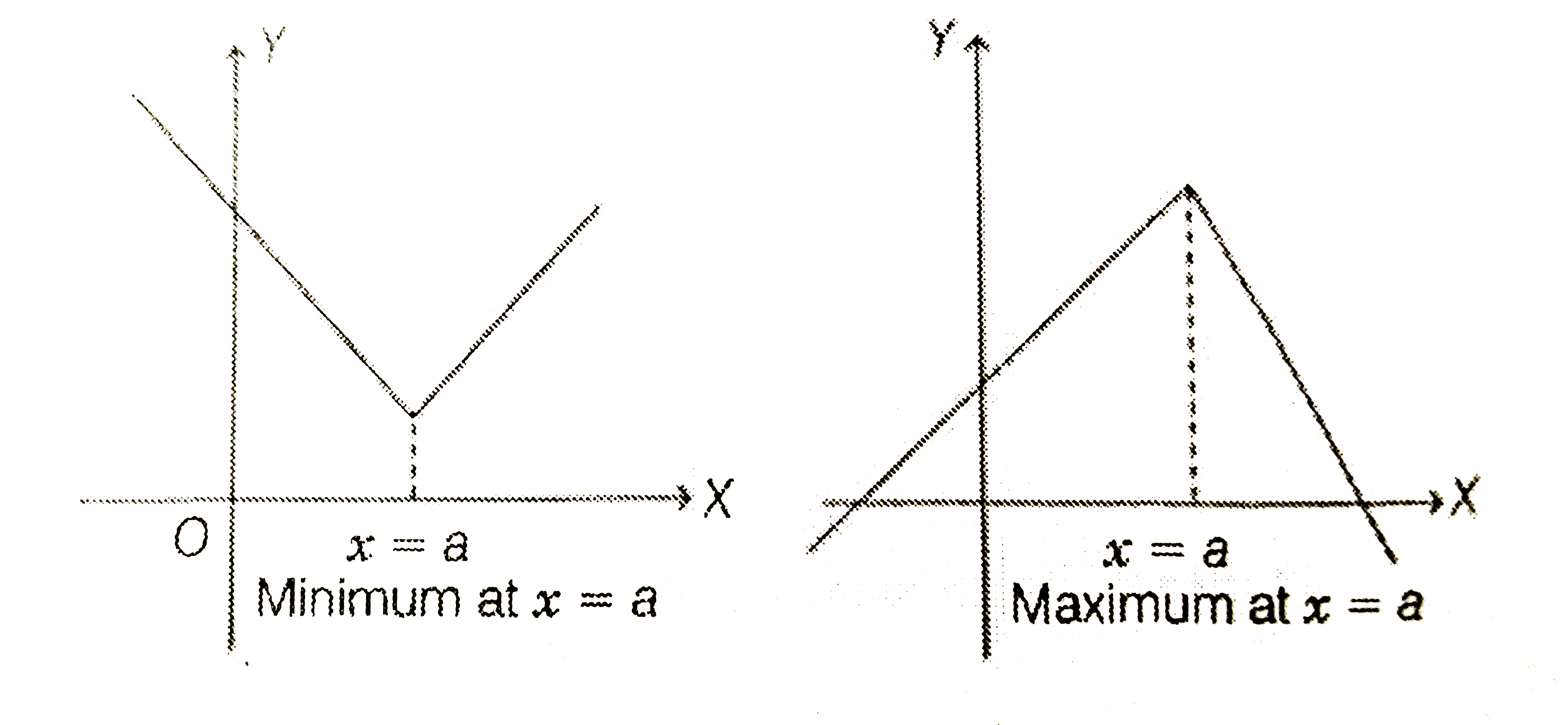Class 12
MATHS
The function f(x)=2|x|+|x+2|=||x|2|-2|x|...

The function `f(x)=2|x|+|x+2|=||x|2|-2|x||` has a local minimum or a local maximum at `x=` `-2` (b) `-2/3` (c) 2 (d) `2/3`

A

`-2 `

B

`(-2)/(3)`

C

` 2`

D

` 2//3`

Text Solution

Verified by Experts

The correct Answer is:
A, D
We know that, ` |x| = {{:(x",",, if x ge0 ),( - x",",, if x lt 0 ):}`
`rArr " " |x- a| = {{:(x- a",",, if x ge a), ( - (x - a)"," ,, if x lt a):}`
and for non - differentiable continuous function, the maximum or minimum can be checked with graph as


Here, `f(x) = 2 |x| + |x + 2| - ||x + 2| - 2 |x||`
`= {{:( - 2x - (x +2) + (x - 2)",",, if when x le - 2 ), ( - 2 x +x +2 + 3x + 2 ",",, if when - 2 lt x le - 2//3 ),( - 4x ",",, if when - (2)/(3) lt x le 0), ( 4x ",",, if when 0 lt x le 2 ), ( 2x + 4",",, if when x gt 2):}`
`= {{:( - 2 x - 4",",, if ,, x le - 2), ( 2x - 4",",, if ,, -2 lt x le - 2//3), ( - 4x ",",, if ,, - (2)/(3) lt x le 0 ), ( 4x",",, if ,, 0 lt x le 2), ( 2x + 4"," ,, if ,, x gt 2):}`
Graph for `y = f (x)` is shown as
Promotional Banner

Similar Questions

Explore conceptually related problems

The function f(x)=2|x|+|x+2|-||x+2|-2|x|| has a local minimum or a local maximum at x equal to:

The function f(x)=x/2+2/x has a local minimum at x=2 (b) x=-2 x=0 (d) x=1

The function f(x)=sqrt((a x^3+b x^2+c x+d)) has its non-zero local minimum and local maximum values at x=-2 and x = 2 , respectively. It 'a is a root of x^2-x-6=0

If the function f(x)=ax e^(-bx) has a local maximum at the point (2,10), then

Find the local maximum and local minimum of f(x) = 2x^(3) + 5x^(2) - 4x

Find the local maximum and local minimum of the function x^(4) - 3x^(3) + 3x^(2) -x

Let f(x)={(|x|,for 0 (a) a local maximum (b) no local maximum (c) a local minimum (d) no extremum

The function f(x)=x(x+4)e^(-x//2) has its local maxima at x=adot Then (a) a=2sqrt(2) (b) a=1-sqrt(3) (c) a=-1+sqrt(3) (d) a=-4

The function f(x)=int_(-1)^x t(e^t-1)(t-1)(t-2)^3(t-3)^5dt has a local minimum at x= 0 (b) 1 (c) 2 (d) 3

The function f(x)=x^2+lambda/x has a (a)minimum at x=2iflambda=16 (b)maximum at x=2iflambda=16 (c)maximum for no real value of lambda (d)point of inflection at x=1iflambda=-1