A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
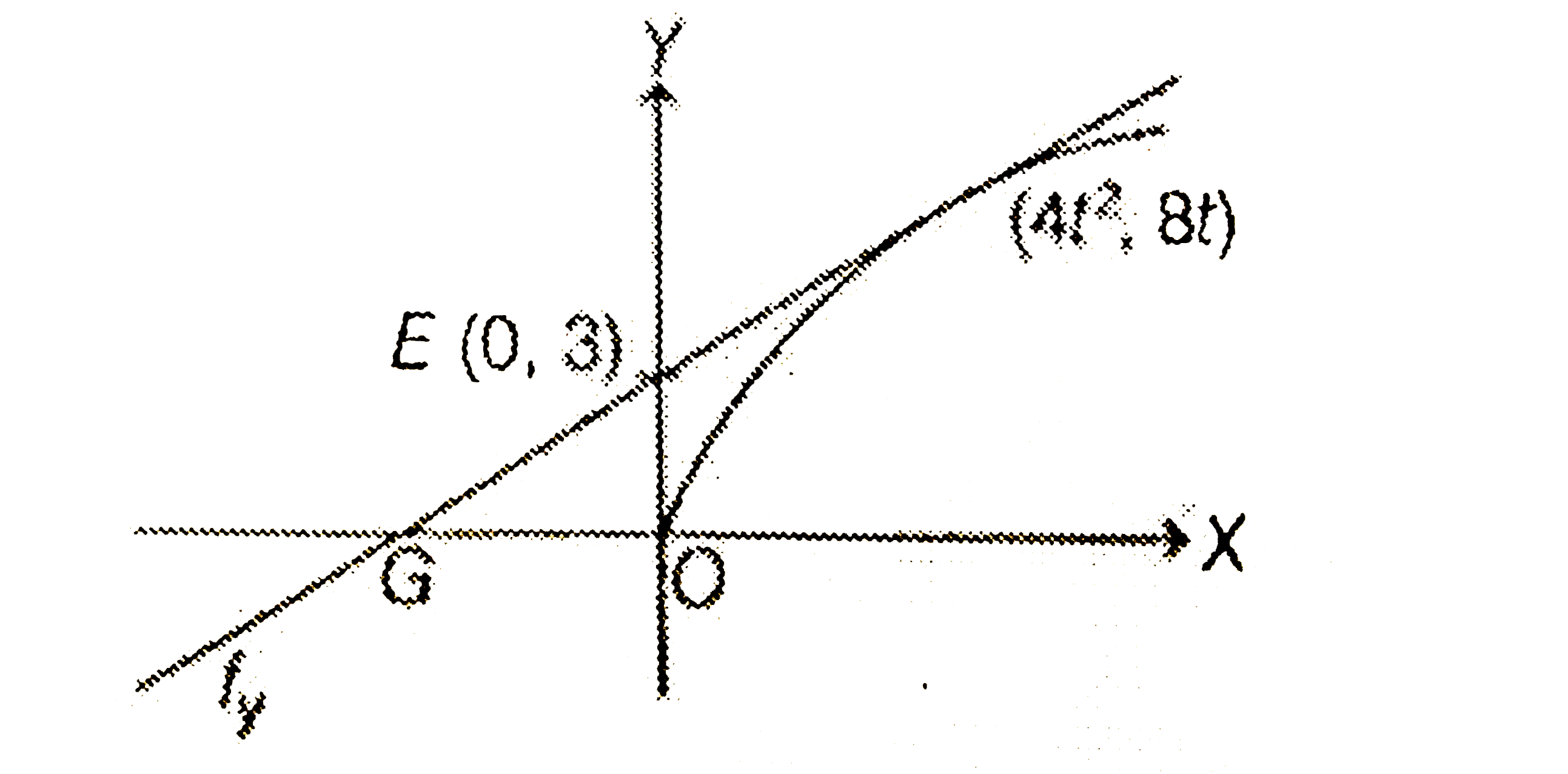
- A line L:y=mx+3 meets y-axis at E(0,3) and the arc of the parabola y ...
Text Solution
|
- Find the value of m for which the lines m x+(2m+3)y+m+6=0 and m x+(2m+...
Text Solution
|
- A line L : y = mx + 3 meets y-axis at E (0, 3) and the arc of the para...
Text Solution
|
- Statement 1: The line x-2y=2 meets the parabola,y^(2)+2x=0 only at the...
Text Solution
|
- Find the equation of the parabola whose focus is at (0, 0) and vertex ...
Text Solution
|
- यदि रेखा x + y = 1 परवलय y^(2) - y + x = 0 को स्पर्श करती है, तो स्पर्...
Text Solution
|
- Area bounded by parabola x^(2)=y, the Y-axis and the lines y = 0, y = ...
Text Solution
|
- m का मान निकालें ताकि निम्नलिखित रेखाएँ y-अक्ष पर एक बिंदु पर प्रतिच्छ...
Text Solution
|
- line L:y=mx+3 meets y–axis at E(0, 3) and the are of the parabola y^(2...
Text Solution
|