Let the squares S is to be bounded by the lines ` x = pm 1//2 and y = pm 1//2`
We have, `" " a ^(2) = ( x_1 - (1)/(2))^(2) + ((1)/(2) - y _1 )^(2)`
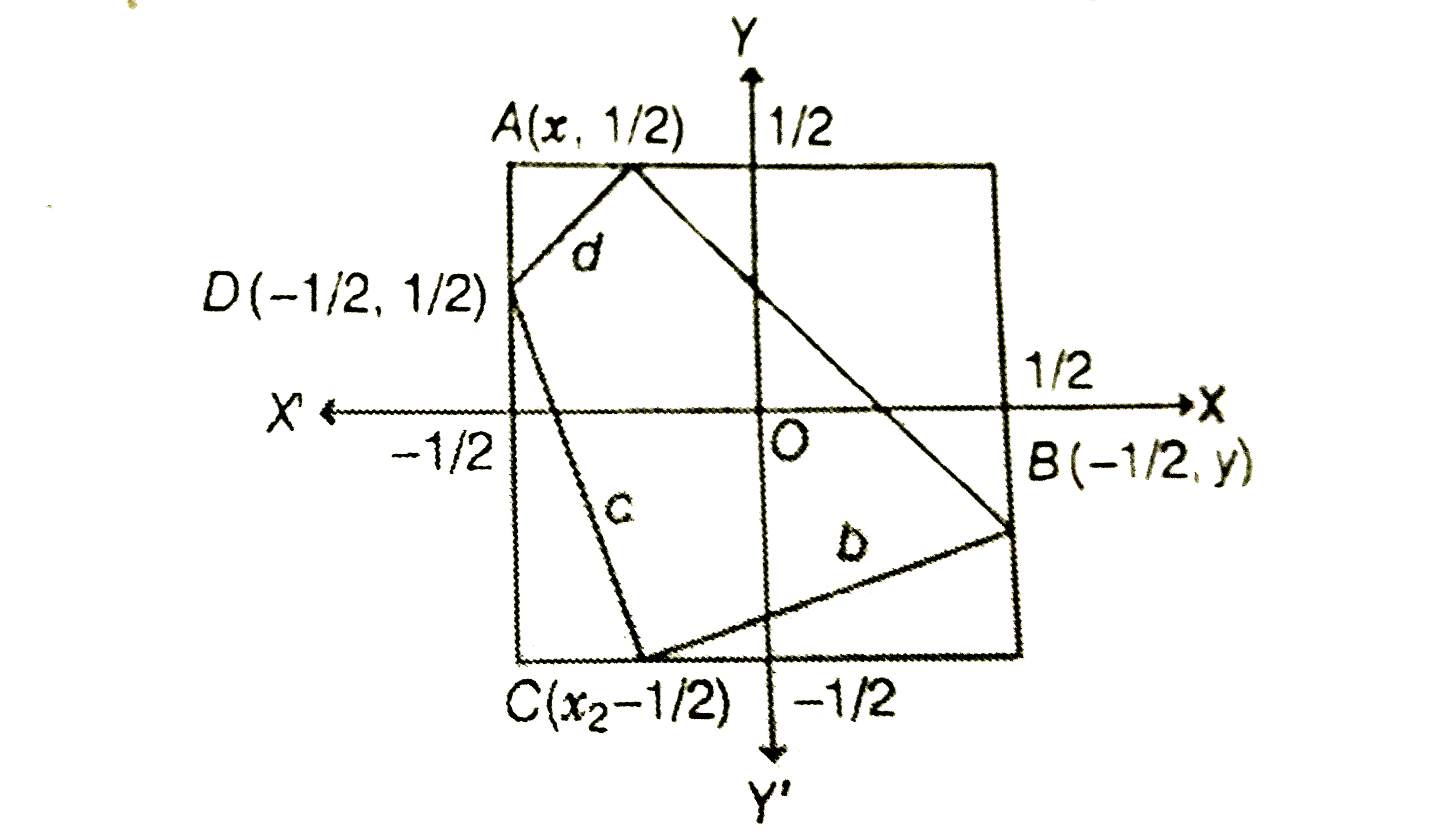
`" " = x_1^(2) - y_1^(2) - x _1 - y _1 + (1)/(2)`
Similarly, ` b ^(2) = x_2^(2) - y _1 ^(2) - x _2 + y _1 + (1)/(2) `
`" " c ^(2) = x _2 ^(2) - y_2^(2) + x _2 + y _2 + (1)/(2)`
`" " d ^(2) = x _1 ^(2) - y_2 ^(2) + x _1 - y _ 2 + (1)/(2)`
`therefore a ^(2) + b ^(2) + c ^(2) + d ^(2) = 2 (x _1 ^(2) + y _ 1^(2) + x _2 ^(2) + y _2 ^(2)) + 2 `
Therefore, `0 le x _1 ^(2), x_2 ^(2), y _1 ^(2), y _2 ^(2) le (1)/(4)`
`" " 0 le x _1 ^(2 ) +x _2 ^(2) + y _1 ^(2) + y _2 ^(2) le 1 `
`rArr " " 0 le 2 (x_1^(2) + x _2 ^(2) + y _1^(2) + y _2 ^(2)) le 2 `
But ` " " 2 le 2 (x _1 ^(2) + x _2 ^(2) + y _1 ^(2) +y _2 ^(2)) + 2 le 4 `
Alternate solution
`c ^(2) = x _2 ^(2) + y _2 ^(2)" " `... (i)
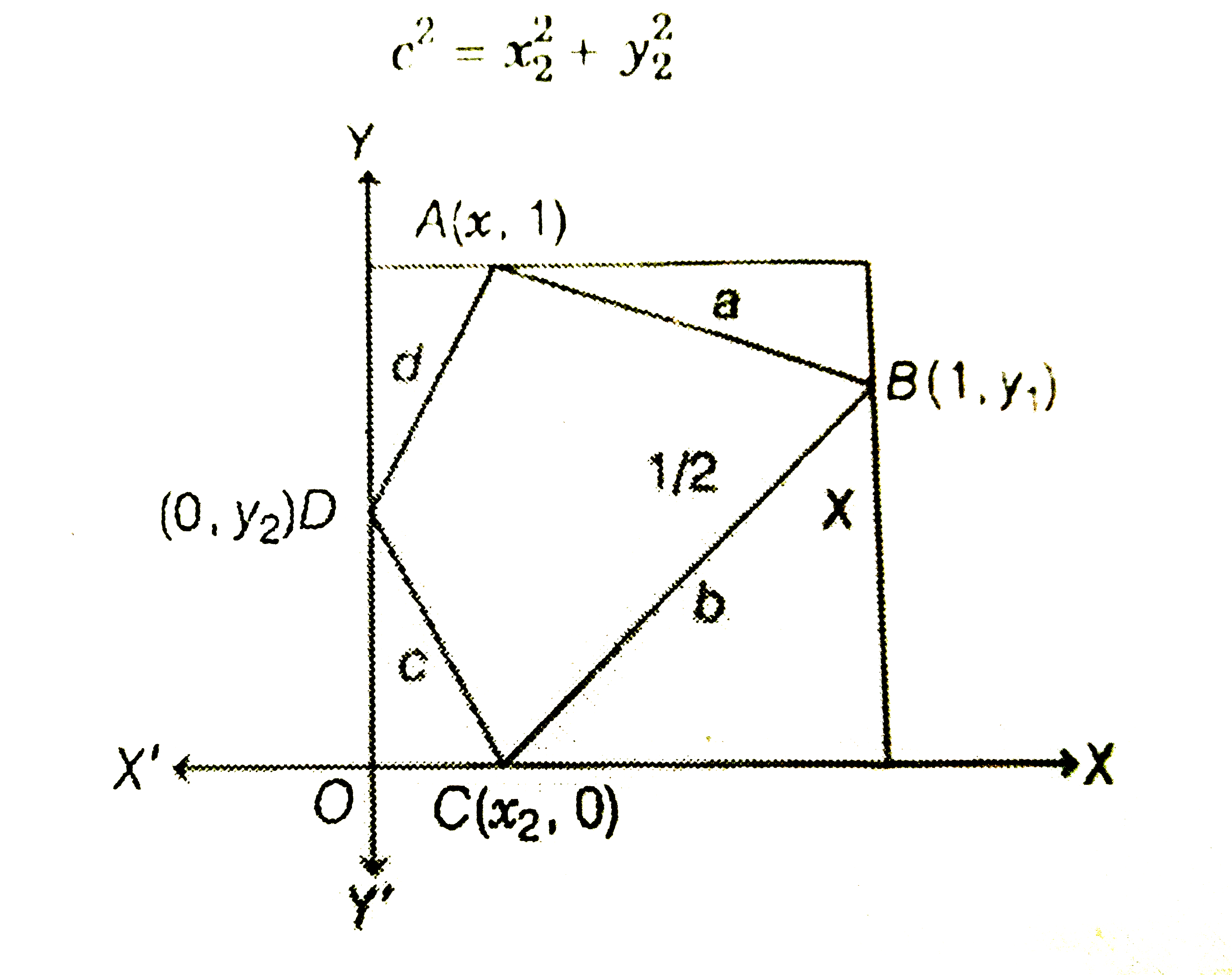
` " " b^(2) = (1 - x _2 ) ^(2) + y _1 ^(2) " " `... (ii)
` " " a^(2) = ( 1 - y_1 ) ^(2) + (1 - x _1 )^(2) " "` ... (iii)
`" " d^(2) = x _1 ^(2) + (1 - y _2) ^(2) " "` ... (iv)
On adding Eqs. (i), (ii), (iii) and (iv), we get
`a ^2 + b ^(2) + c ^(2) + d ^(2) = { x _1 ^(2) + (1 - x _1 ) ^(2) } + { y_1 ^(2) + (1 - y _1 ) ^(2) } + { x_2 ^(2) + (1 - x _2 ) ^(2)} + { y _2 ^(2) + (1 -y_2 ) ^(2)} `
where ` x _1 , y _1 , x_2, y _2 ` all vary in the interval ` [ 0, 1]`
Now, consider the function `y = x ^(2) + ( 1 - x^(2)), 0 le x le 1 `
differentiating `rArr (dy )/(dx) = 2x -2 ( 1-x) `. For maximum or minimum ` (dy)/(dx)= 0`.
`rArr 2x - 2 ( 1- x ) = 0 rArr 2x -2 + 2 x = 0`
`rArr 4x = 2 " " rArr x = 1 //2 `
Again, ` " " (d ^(2) y)/(dx^(2)) = 2 + 2 = 4 `
Hence, `y ` is minimum at ` x = (1)/(2)` and its minimum value is ` 1//4`. Clearly, value is maximum when ` x = 1`.
`therefore` Minimum value of ` a^(2) + b ^(2) + c ^(2) + d ^(2) = (1)/(2) + (1)/(2) + (1)/(2) + (1)/(2) = 2 `
and maximum value is ` 1+ 1 + 1 +1 = 4 `

