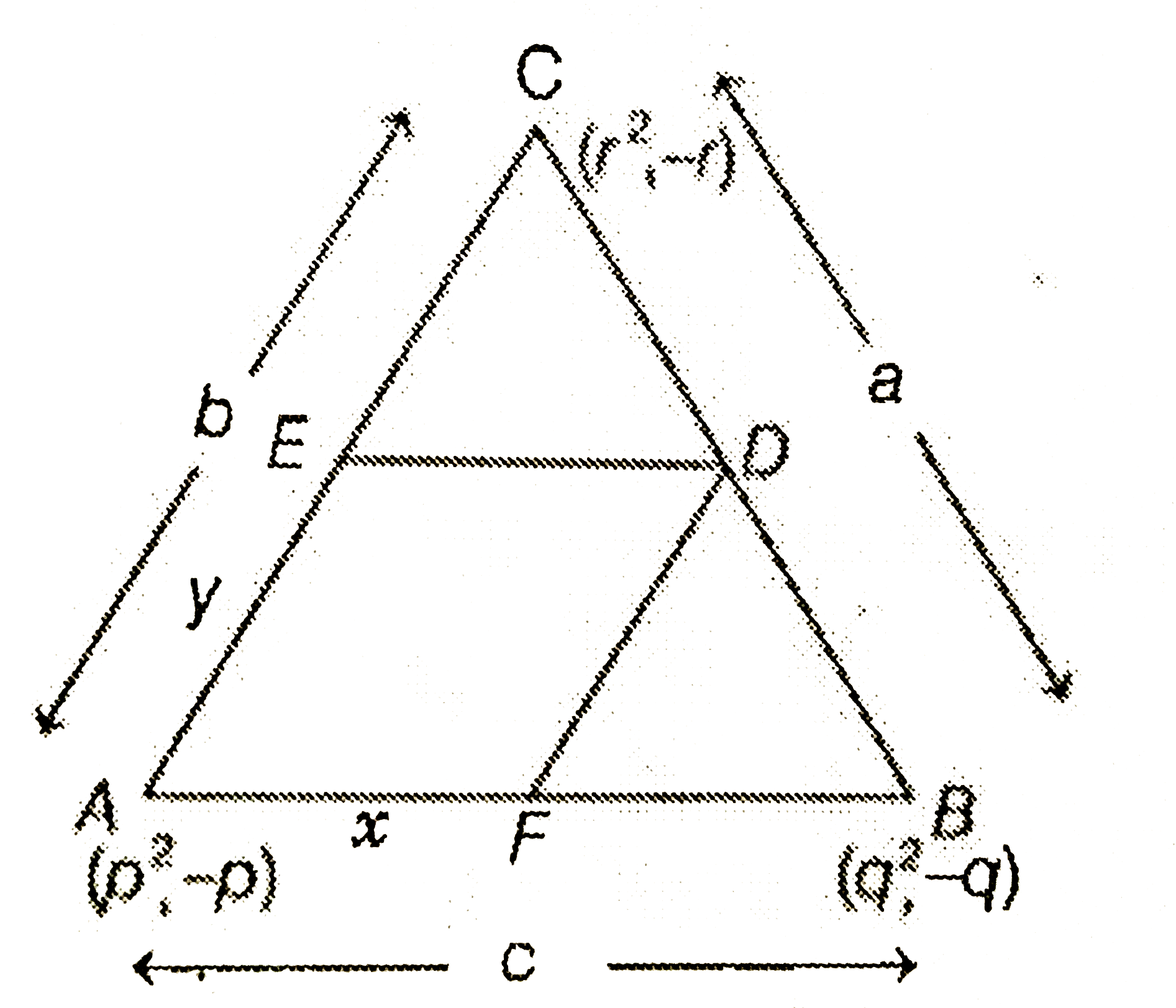Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let A(p^2,-p),B(q^2, q),C(r^2,-r) be the vertices of triangle ABC. A p...
Text Solution
|
- In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q...
Text Solution
|
- If (x+2) is a common factor of (px^(2)+qx+r) and (qx^(2)+px+r) then a ...
Text Solution
|
- Let A(p^2,-p),B(q^2, q),C(r^2,-r) be the vertices of triangle ABC. A p...
Text Solution
|
- If p,q,r are in A.P the p^(2)(q+r),q^(2)(r+p),r^(2)(p+q) are in
Text Solution
|
- In a Delta ABC, if p,q,r are the distances from the orthocentre to the...
Text Solution
|
- ಒಂದು ಸಮಾಂತರ ಶ್ರೇಡಿಯ p ನೇ q ನೇ ಮತ್ತು r ನೇ ಪದಗಳು ಕ್ರಮವಾಗಿ a,b ಶಮತ್ತು c ಗ...
Text Solution
|
- In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q...
Text Solution
|
- Let A(p^2,-p),B(q^2, q),C(r^2,-r) be the vertices of triangle ABC. A p...
Text Solution
|