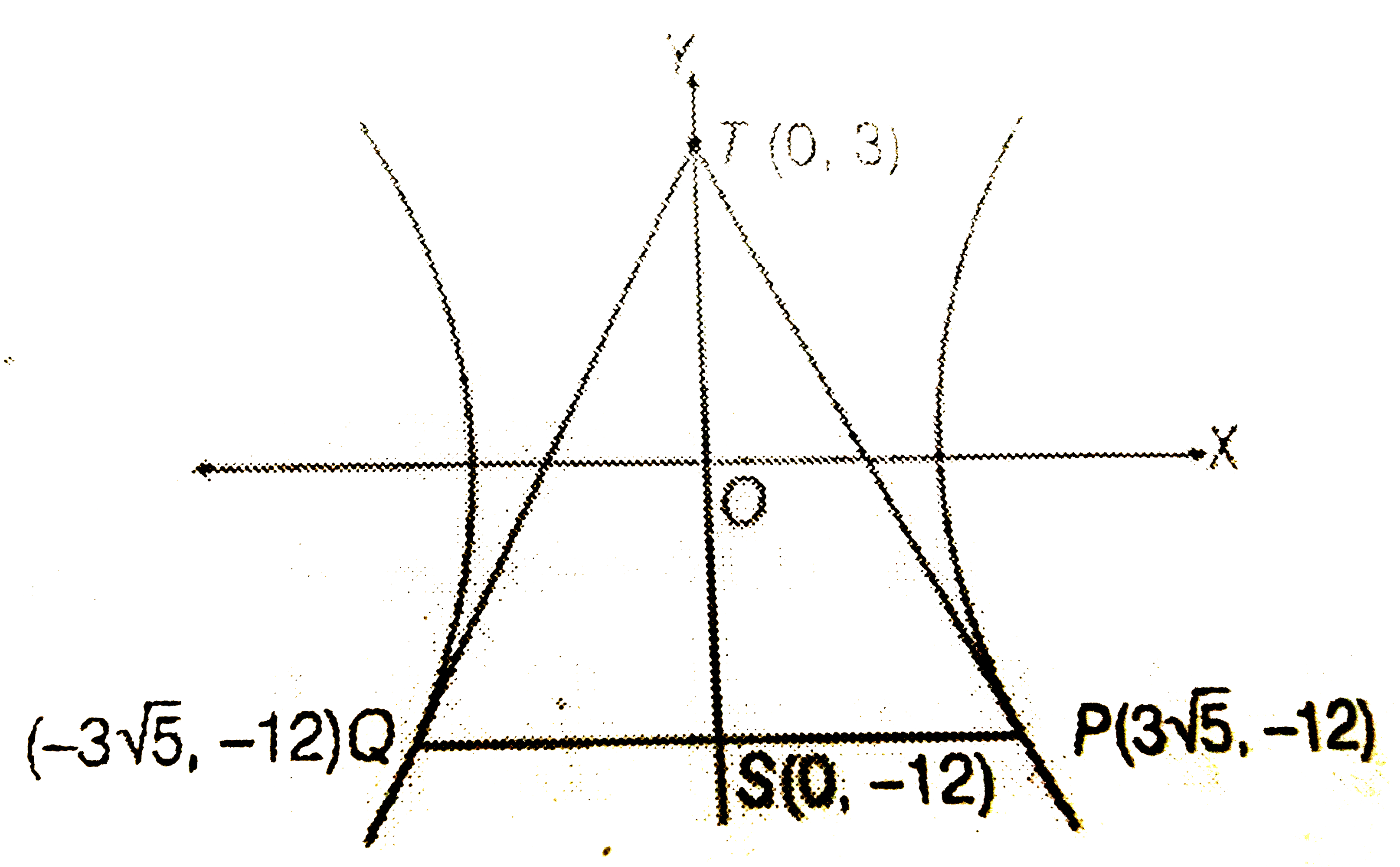A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Tangents are drawn to the hyperbola 4x^2-y^2=36 at the points P and Q....
Text Solution
|
- Tangents are drawn to the hyperbola 4x^2-y^2=36 at the points P and Q....
Text Solution
|
- A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2...
Text Solution
|
- एक अतिपरवलय 4x^(2)-y^(2)=36 के बिंदुओं P तथा Q पर स्पर्श रेखाएँ खींची ...
Text Solution
|
- Tangents are drawn to the hyperbola 4x^(2)-y^(2)=36 at the points P a...
Text Solution
|
- The normal at a point P to the parabola y^(2) = 4x is parallel to the ...
Text Solution
|
- Tangents are drawn to the hyperbola 4x^2-y^2=36 at the points P and Q....
Text Solution
|
- A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2...
Text Solution
|
- Tangents are drawn to the hyperbola 4x^2-y^2=36 at the points P and Q....
Text Solution
|