Home
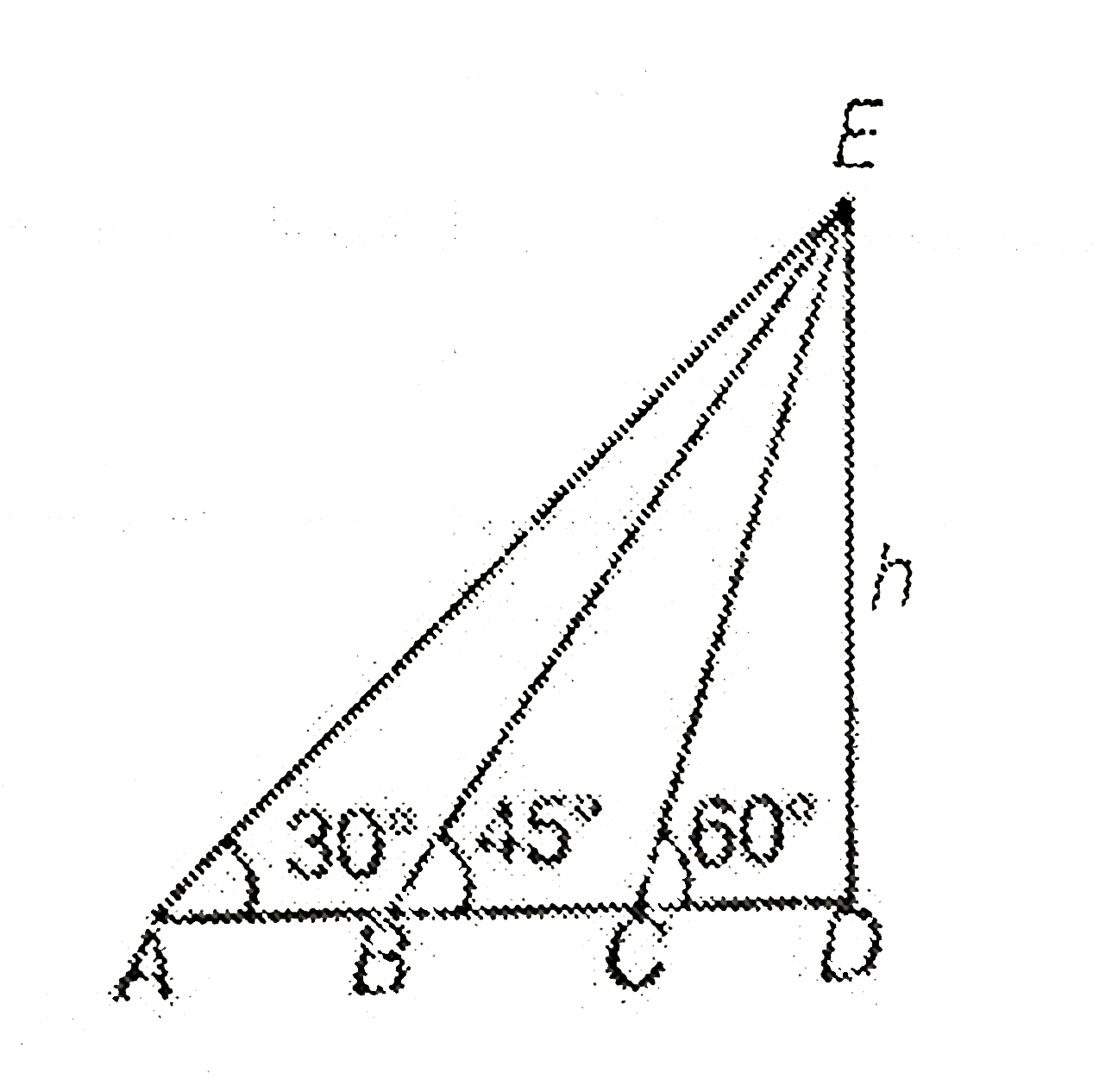
Class 12
MATHS
If the anlges of elevation of the top of...

If the anlges of elevation of the top of a tower from three collinear points A,B and C on a line leading to the foot of the tower are `30^@ , 45^@ "and " 60 ^@` respectively , then the ratio AB:BC is

A

`sqrt(3) : 1`

B

`sqrt(3):sqrt(2)`

C

`1:sqrt(3)`

D

`2:3`

Text Solution

Verified by Experts

The correct Answer is:
A
According to the given information, the figure should be as follows:
Let the height of tower `= h`
In `triangle EDA, tan 30^(@)=(ED)/(AD)`
`(1)/(sqrt(3))=(ED)/(AD)=(h)/(AD)`
`rArr AD = h sqrt(3)`

In ` triangle EDB, tan 45^(@) = (h)/(BD) rArr BD=h`
In ` triangle EDC, tan 60^(@) = (h)/ (CD) rArr CD= (h)/(sqrt(3))`
Now, `(AB)/(BC) =(AD-BD)/(BD-CD) rArr (AB)/(BC) = (h sqrt(3)-h)/(h-(h)/(sqrt(3)))`
`rArr (AB)/(BC)=(h(sqrt(3)-1))/((h(sqrt(3)-1))/(sqrt(3))) rArr (AB)/(BC)=(sqrt(3)-1)/((sqrt(3)-1))xxsqrt(3)`
`rArr (AB)/(BC)=(sqrt(3))/(1) therefore AB: BC=sqrt(3) : 1`
Promotional Banner

Similar Questions

Explore conceptually related problems

If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 30^0 , 45^0 and 60^0 respectively, then the ratio, AB : BC, is : (1) sqrt(3):1 (2) sqrt(3):sqrt(2) (3) 1:sqrt(3) (4) 2"":""3

The angle elevation of the top of a tower from a point C on the ground. Which is 30 m away from the foot of the tower is 30^(@) . Find the height of the tower.

Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away the foot of a tower of height 10sqrt(3) m.

The angle of elevation of the top of a tower from a point O on the ground, qhich is 450 m away from the foot of the tower, is 40^(@) . Find the height of the tower.

If the angle of elevation of the top of a tower at a distance 500 metres from its foot is 30^@ then the height of the tower is

The angle ofelevation of the top of a tower from the foot of the building is 30^(@) and the angle of elevation of the top of the building from the foot of the tower is 60^(@) . What is the ratio ofheights of tower and building.

A TV tower stands vertically on a bank of a canal. The tower is watched from a point on the other bank directly opposite to it. The angle of elevation of the top of the tower is 58^(@) . From another point 20m away from this point on the line joining this point to the foot of the tower , the angle of elevation of the top of the tower is 30^(@) . Find the height of the tower and the width of the canal . (tan 58^@ = 1.6003)

The angle of elevation of the top of a building from the foot of the tower is 30^(@) and the angle of elevation of the top of the tower from the foot of the building is 60^(@) . If the tower is 30 m high, find the height of the building.