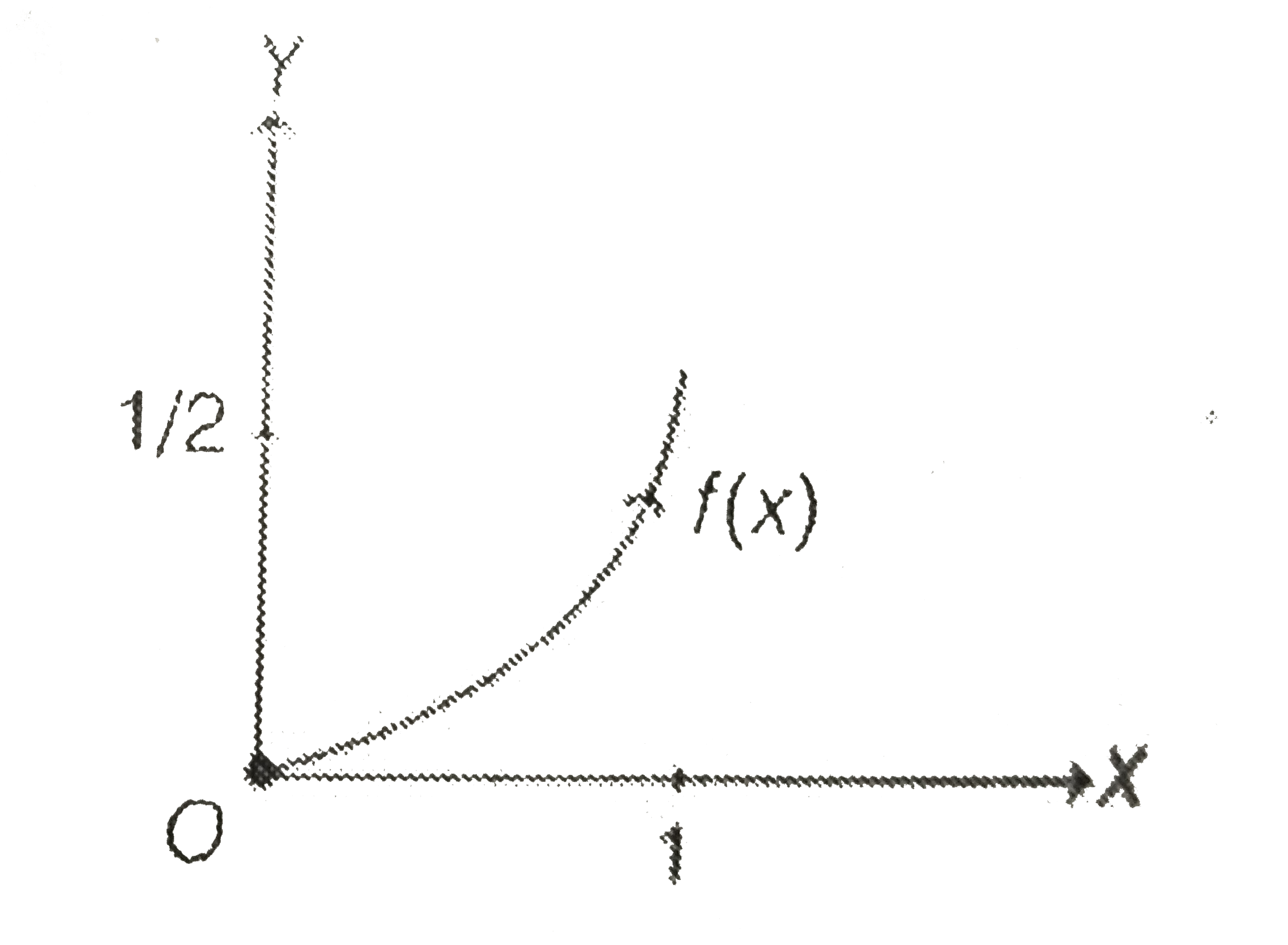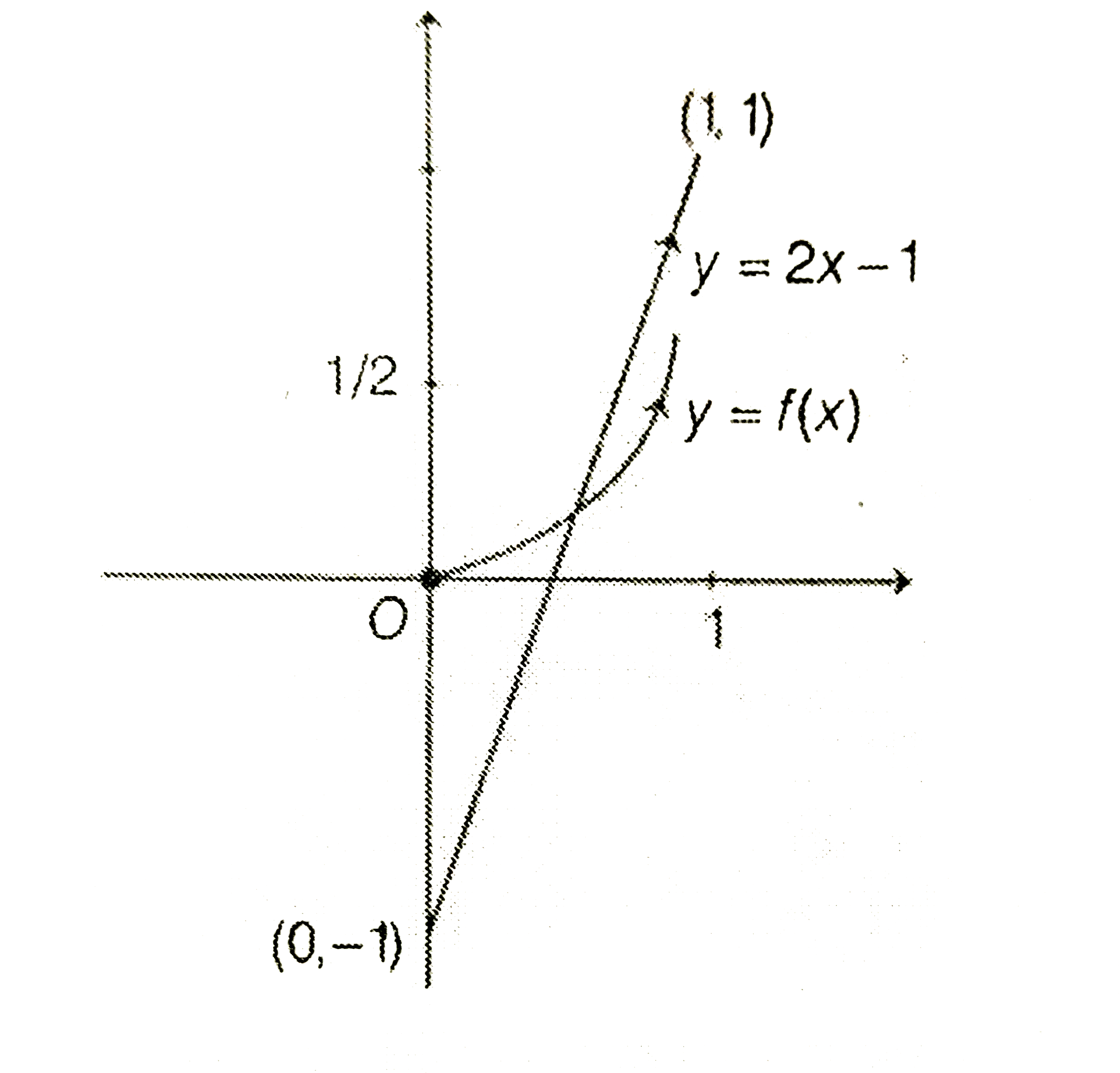Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The total number for distinct x epsilon[0,1] for which int(0)^(x)(t^(2...
Text Solution
|
- If int(0)^(x)f(t)dt=x^(2)+int(x)^(1)t^(2)f(t)dt, then f'((1)/(2)) is
Text Solution
|
- Total number of distinct x epsilon [0,1] for which int(0)^(x) (t^(8)+1...
Text Solution
|
- If int(0)^(x)f(t)dt = x^(2)-int(0)^(x^(2))(f(t))/(t)dt then find f(1).
Text Solution
|
- The total number of distinct x in (0,1] for which int(0)^(x)(t^(2))/...
Text Solution
|
- The total number for distinct x in[0,1] for which int(0)^(x)(t^(2))/(1...
Text Solution
|
- If int(0)^(x)f(t)dt=e^(x)-ae^(2x)int(0)^(1)f(t)e^(-t)dt, then
Text Solution
|
- If f(x)=int(0)^(x) {f(t)}^(-1)dt, " and " int(0)^(1) {f(t}^(-1)dt=sqrt...
Text Solution
|
- The function f:[0,1]rarr R is continuous on [0,1] and int(0)^(x)f(t)dt...
Text Solution
|