Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
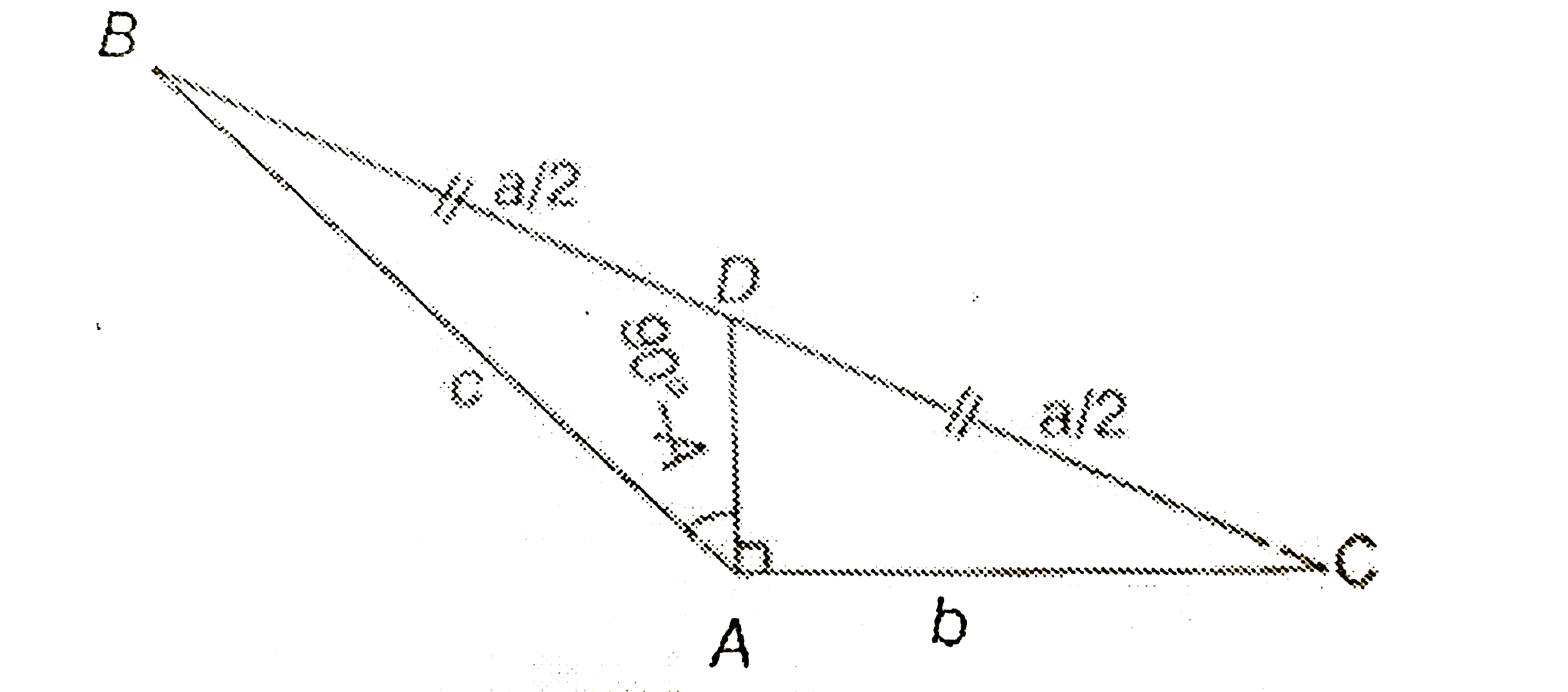
- ABC is triangle. D is the middle point of BC. If AD is perendicular to...
Text Solution
|
- D is midpoint of BC in Delta ABC such that AD and AC are perpendicular...
Text Solution
|
- A B C is a triangle in which A B=A C and D is any point in B C ....
Text Solution
|
- ABC is triangle. D is the middle point of BC. If AD is perendicular to...
Text Solution
|
- In an isoscles Delta ABC, AB= AC and D is a point on BC. Prove that AB...
Text Solution
|
- एक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध...
Text Solution
|
- ABC is a triangle and D is the middle point of BC. If AD is perpendicu...
Text Solution
|
- एक में, भुजा BC का मध्य बिंदु D है । यदि AD भुजा AC के लंबवत है, ...
Text Solution
|
- triangleABC में, D भुजा BC का मध्यबिन्दु है। यदि ADbotAC तो सिद्ध कीजि...
Text Solution
|