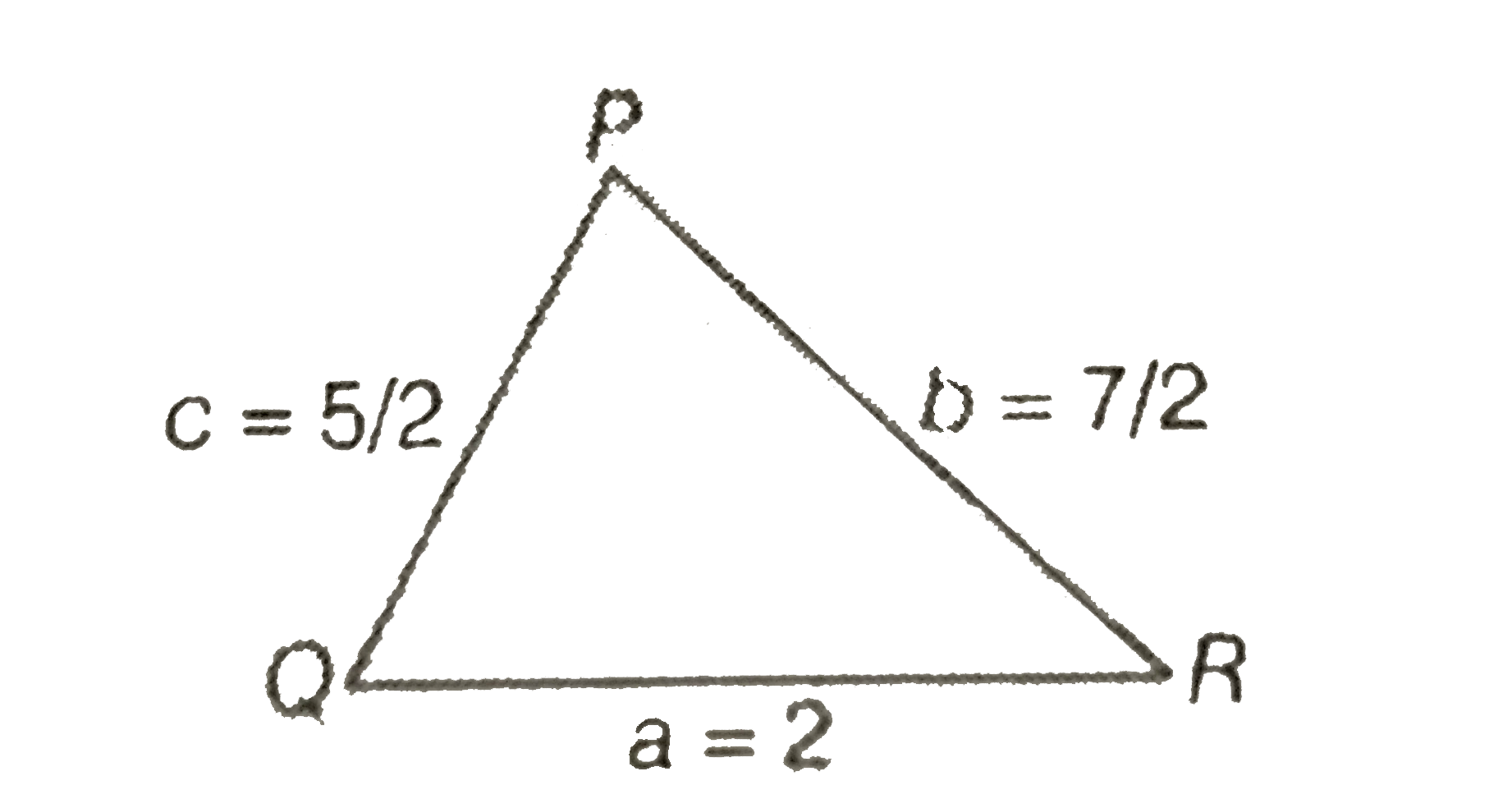A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let P Q R be a triangle of area with a=2,b=7/2,a n dc=5/2, w h e r ea...
Text Solution
|
- Let P Q R be a triangle of area with a=2,b=7/2,a n dc=5/2, w h e r ea ...
Text Solution
|
- Let PQR be a triangle of area Delta with a=2,b=(7)/(2) and c=(5)/(2), ...
Text Solution
|
- The following are the steps in finding the matrix B, if B + ({:(2, 3),...
Text Solution
|
- Let PQR be a triangle of ! area with a = 2 , b = 7/2 and c = 5/2, wher...
Text Solution
|
- Let PQR be a triangle of area Delta with a=2, b=(7)/(2) and c=(5)/(2),...
Text Solution
|
- Let P Q R be a triangle of area with a=2,b=7/2,and c=5/2, where a, b a...
Text Solution
|
- If a ,b ,a n dc are in A.P. p ,q ,a n dr are in H.P., and a p ,b q ,a ...
Text Solution
|
- If a ,b ,a n dc are in A.P. p ,q ,a n dr are in H.P., and a p ,b q ,a ...
Text Solution
|