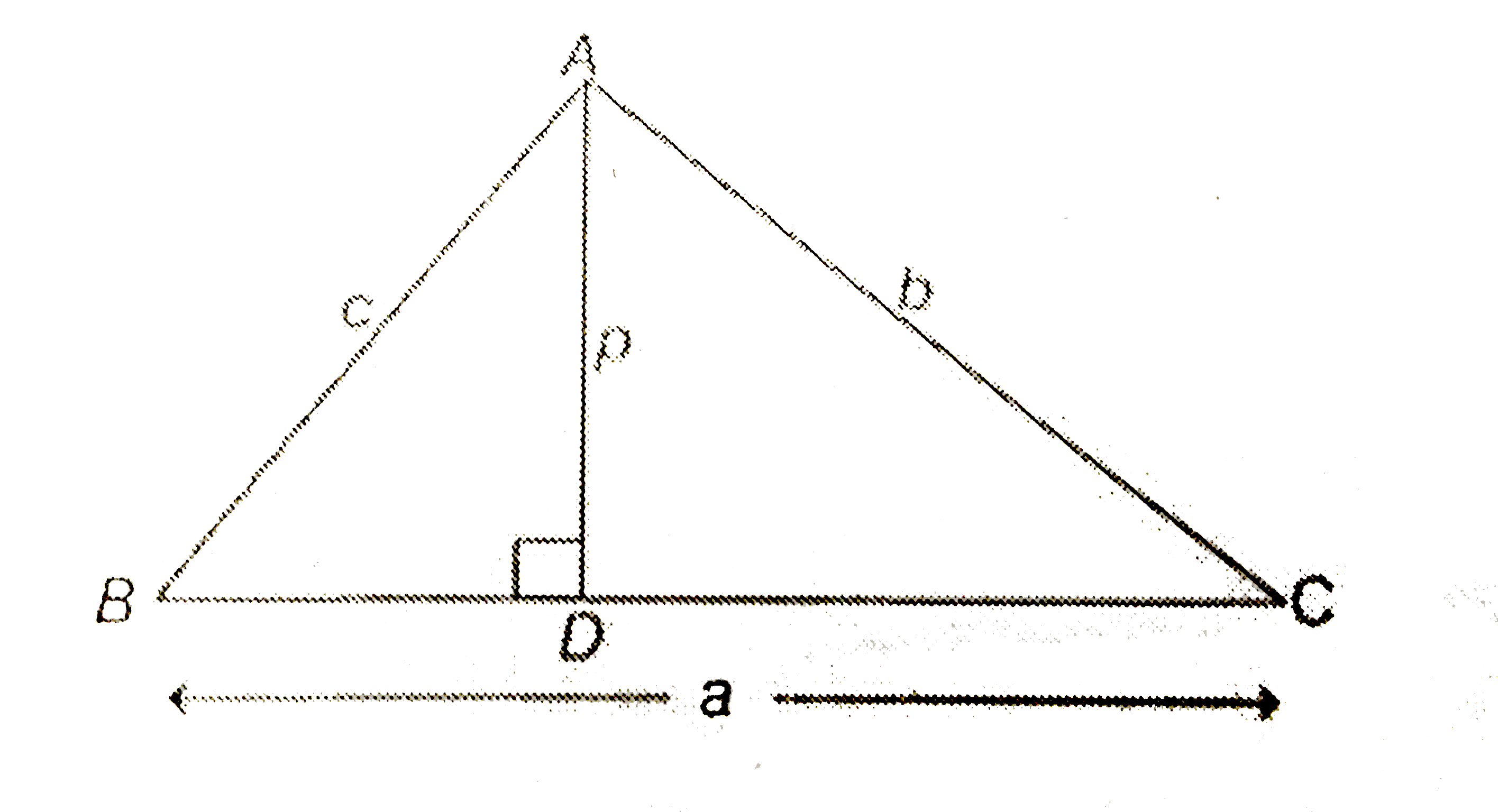Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a triangle of base a , the ratio of the other two sides is r(<1)dot...
Text Solution
|
- If the sides of triangle ABC are in G.P.with common ratio r(r<1), show...
Text Solution
|
- If in a triangle of base 'a', the ratio of the other two sides is r ( ...
Text Solution
|
- In a triangle of base a, the ratio of the other two sides is r (lt 1)....
Text Solution
|
- The altitude of a right triangle is 7 cm less than its base. If the h...
Text Solution
|
- आधार a के किसी त्रिभुज में अन्य दो भुजाओं का अनुपात r (r lt 1) है। प्...
Text Solution
|
- The altitude of a right triangle is 7 cm less than its base. If the hy...
Text Solution
|
- The altitude of a right triangle is 7 cm less than its base. If the hy...
Text Solution
|
- The altitude of a right triangle is 7 cm less than its base. If the hy...
Text Solution
|