A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The value of int0^(2pi)[2 sin x] dx, where [.] represents the greate...
Text Solution
|
- The value of int(0)^(2 pi)[2sin x]dx, where [.] represents the greates...
Text Solution
|
- The value of int(pi)^(2pi) [ 2 sin x] dx, where [] repreents the great...
Text Solution
|
- The value of intx^(2pi) [2 sin x] dx,where [x] represents the greatest...
Text Solution
|
- int0^(2pi)(sinx +cosx)dx সমাকলের মান হয়—
Text Solution
|
- The value of integrals int(-2)^(2)max {x+|x|, x-[x]}dx where [.] repre...
Text Solution
|
- int(0)^(2pi) [sin 2x(1+cos 3x)]dx, का मान है, जहाँ [t] महत्तम पूर्णांक...
Text Solution
|
- The value of int0^(2pi)[2sinx]dx ,w h e r e[dot] represents the great...
Text Solution
|
- Evaluate: int0^(100)x-[x]dx where [dot] represents the greatest in...
Text Solution
|
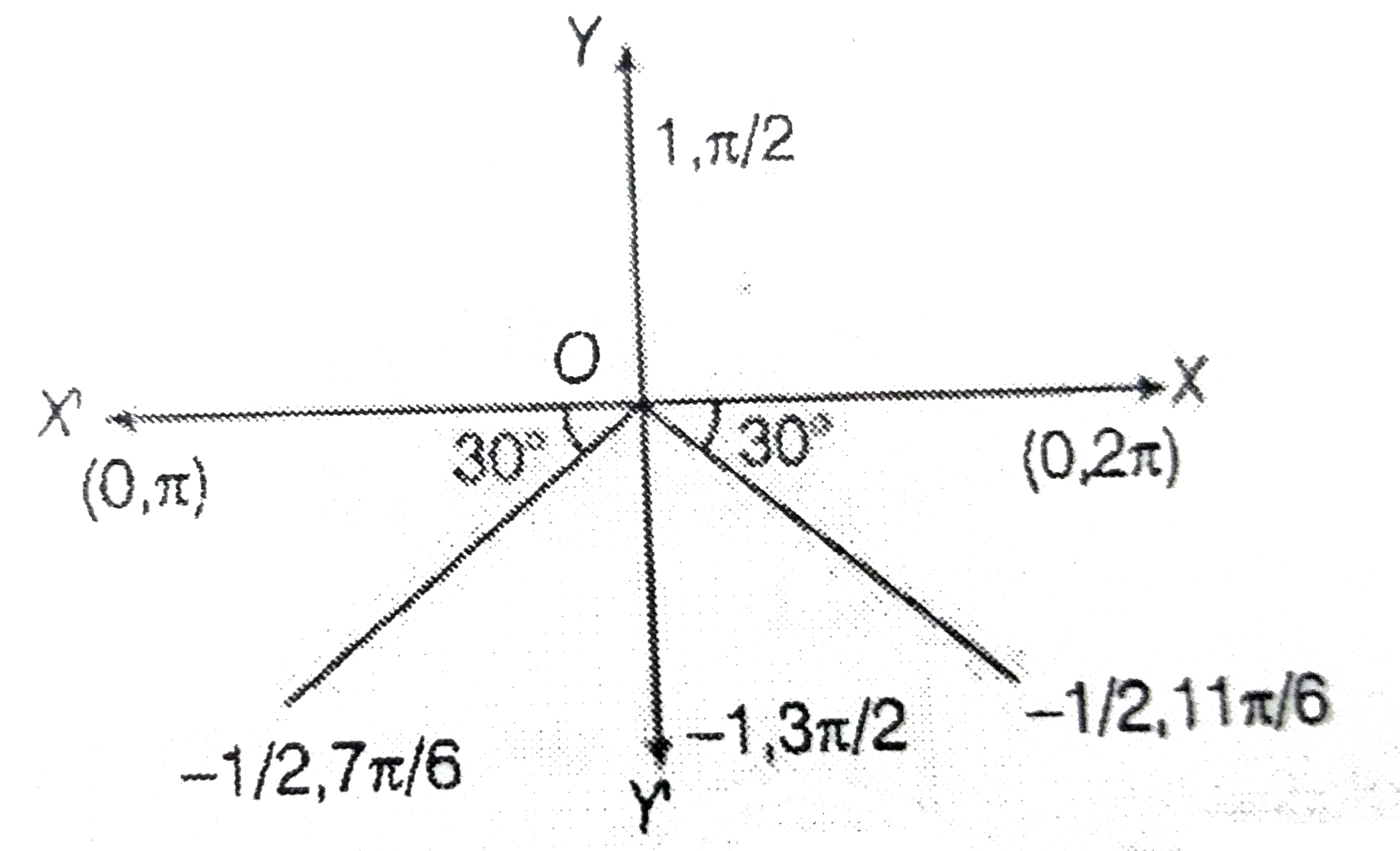 We know that , `"sin" (pi)/(6)=(1)/(2)`
We know that , `"sin" (pi)/(6)=(1)/(2)`