Home
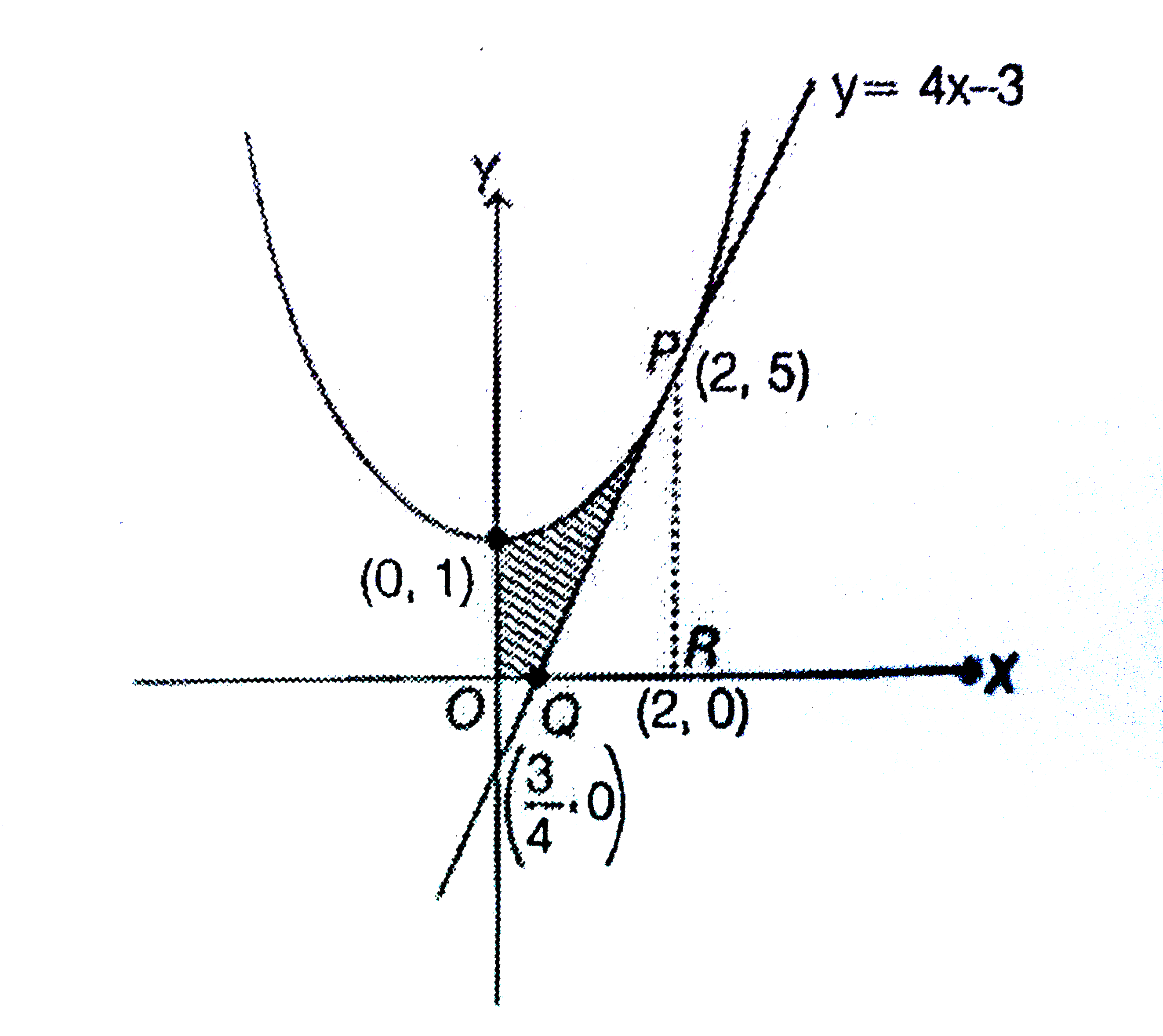
Class 12
MATHS
The area (in sq. units) in the first qua...

The area (in sq. units) in the first quadrant bounded by the parabola `y=x^2+1`, the tangent to it at the point (2, 5) and the coordinate axes is

A

`(14)/(3)`

B

`(187)/(24)`

C

`(8)/(3)`

D

`(37)/(24)`

Text Solution

Verified by Experts

The correct Answer is:
D
Given, equation of parabola is `y=x^(2)+1,` which can be written as `x^(2)=(y-1)`. Clearly, vertex of parabola si (0,1) and it will open upward.
Now, equation of tangent at (2, 5) is `(y+5)/(2)=2x+1`
[`because` Equation of the tangent at `(x_(1),y_(1))` is given by `T=0. " Here, "(1)/(2)(y+y_(1))=x x_(1)+1`]
`y=4x-3`

Required area = Area of shaded region
`=int_(0)^(2) y("parabola")dx-("Area of "Delta PQR)`
`=int_(0)^(2)(x^(2)+1)dx-("Area of "Delta PQR)`
`=((x^(3))/(3)+x)_(0)^(2)-(1)/(2) (2-(3)/(4))*5`
`[because " Area of a triangle "=(1)/(2) xx "base"xx"height"]`
`=((8)/(3)+2)-0-(1)/(2)((5)/(4))5`
`=(14)/(3)-(25)/(8)=(112-75)/(24)=(37)/(24)`
Promotional Banner

Similar Questions

Explore conceptually related problems

The area (in sq. units) bounded by the parabola y=x^2-1 , the tangent at the point (2,3) to it and the y-axis is

The area of the region bounded by the parabola (y-2)^(2) = x- 1 , the tangent to the parabola at the point (2,3) and the x-axis is

Find the area bounded by the parabola y=x^2+1 and the straight line x+y=3.

The area bounded by the parabola y = x^(2) and the line y = 2x is

Find the area lying in the first quadrant and bounded by the curve y=x^3 and the line y=4xdot

The area (in sq. units) of the region bounded by the parabola y=x^2+2" and the lines " y=x+1, x=0 " and " x=3 , is

Find the area of the region if the first quadrant bounded by the parabola y^(2)=4x , the line x+y=3 and y-axis.

The area bounded by the parabola y^(2) = x and its latus rectum is

The area bounded by the parabola x^2=y and is latus rectum is :