A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
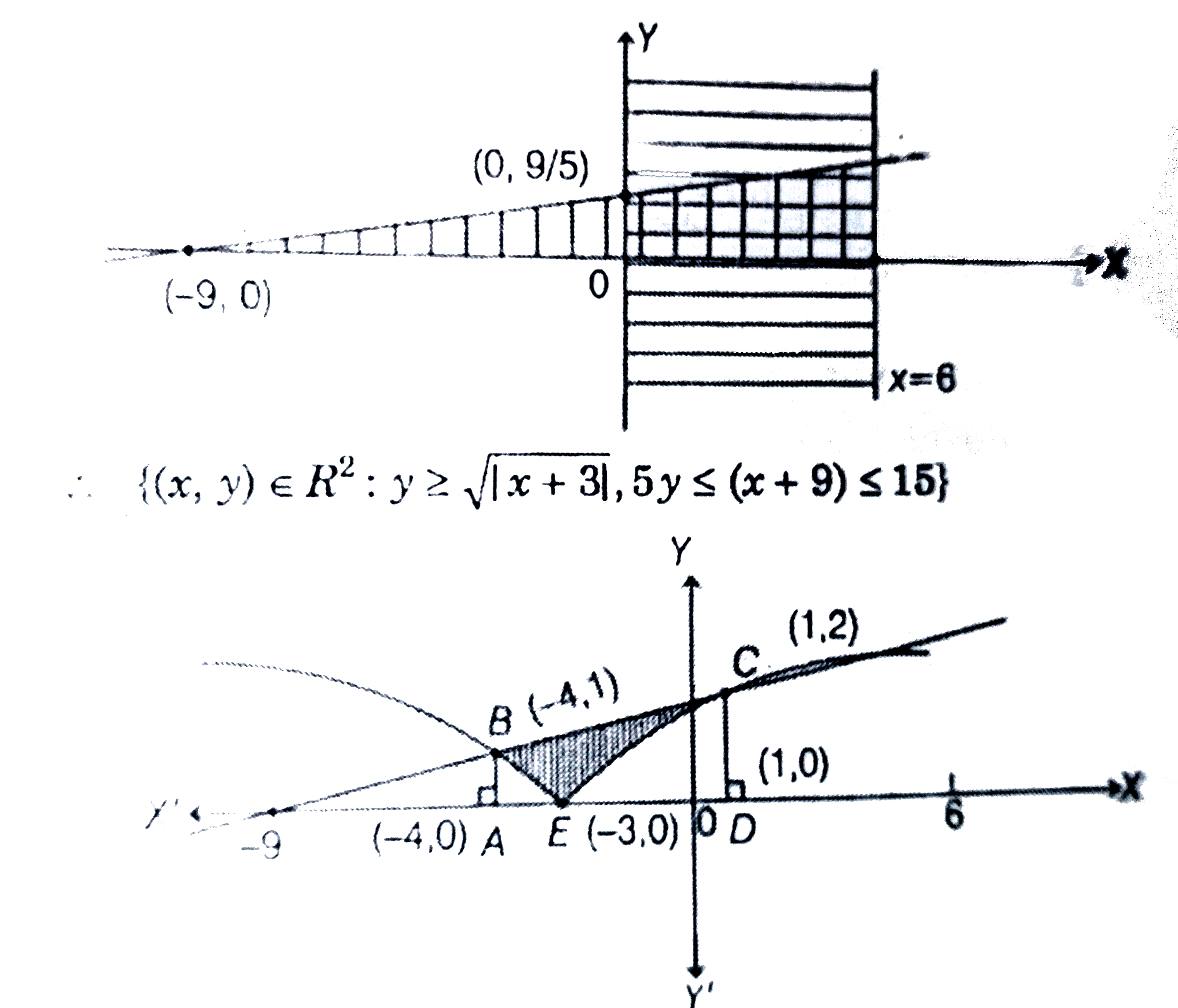
- Area of the region {(x,y) in R^(2):ygesqrt(|x+3|),5ylex+9le15} is eq...
Text Solution
|
- Area bounded by the region R-={(x,y):y^(2)lexle|y|} is
Text Solution
|
- If the line x= alpha divides the area of region R={(x,y)in R^(2): x^(...
Text Solution
|
- The area of the region bounded by the curve y = x^(2) and y = x is equ...
Text Solution
|
- The area of the region bounded by the curve y = x^(2) and y = |x| is ...
Text Solution
|
- क्षेत्र (region) {(x,y) in R^(2): y gesqrt(|x+3)|),5yle x + 9 le 15} क...
Text Solution
|
- Consider a region R={(x,y) in R^(2):x^(2) le y le 2x}. If a line y= al...
Text Solution
|
- The area of the region bounded by x,y in R x^(2)<=y<=2x is
Text Solution
|
- वक्र |x|+|y|+|x-y|le4,|x|le1,ygesqrt(x^(2)-2x+1)से घिरे क्षेत्र का क्ष...
Text Solution
|