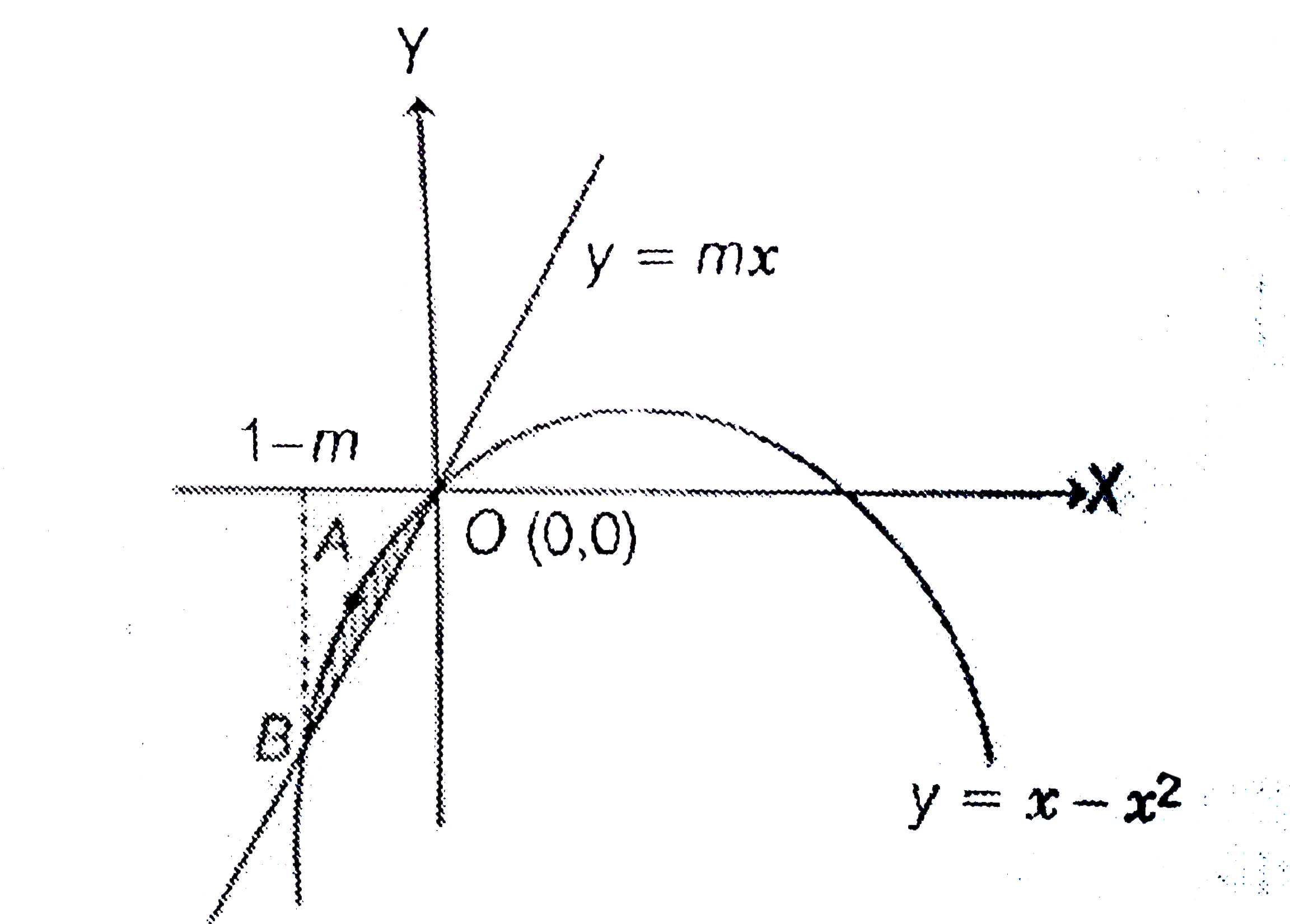A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For which of the following values of m is the area of the regions boun...
Text Solution
|
- For which of the following values of m is the area of the regions bou...
Text Solution
|
- If the area bounded by the curves y=x-x^(2) and line y=mx is equal to ...
Text Solution
|
- Area of the region bounded by the curve y=x^(2),y=|2-x^(2)| and y=2, w...
Text Solution
|
- Find the area of the region bounded by the curves x^(2)+y^(2)=4 and (x...
Text Solution
|
- The area of the region bounded by the curve y = x^(2) and y = x is equ...
Text Solution
|
- The area of the region bounded by the curve y = x^(2) and y = |x| is ...
Text Solution
|
- The area of the region bounded by the curves {(x,y) : x^(2) + y^(2) le...
Text Solution
|
- Area of the region bounded by the curve y={{:(x^(2)",",x lt0),(x",",...
Text Solution
|