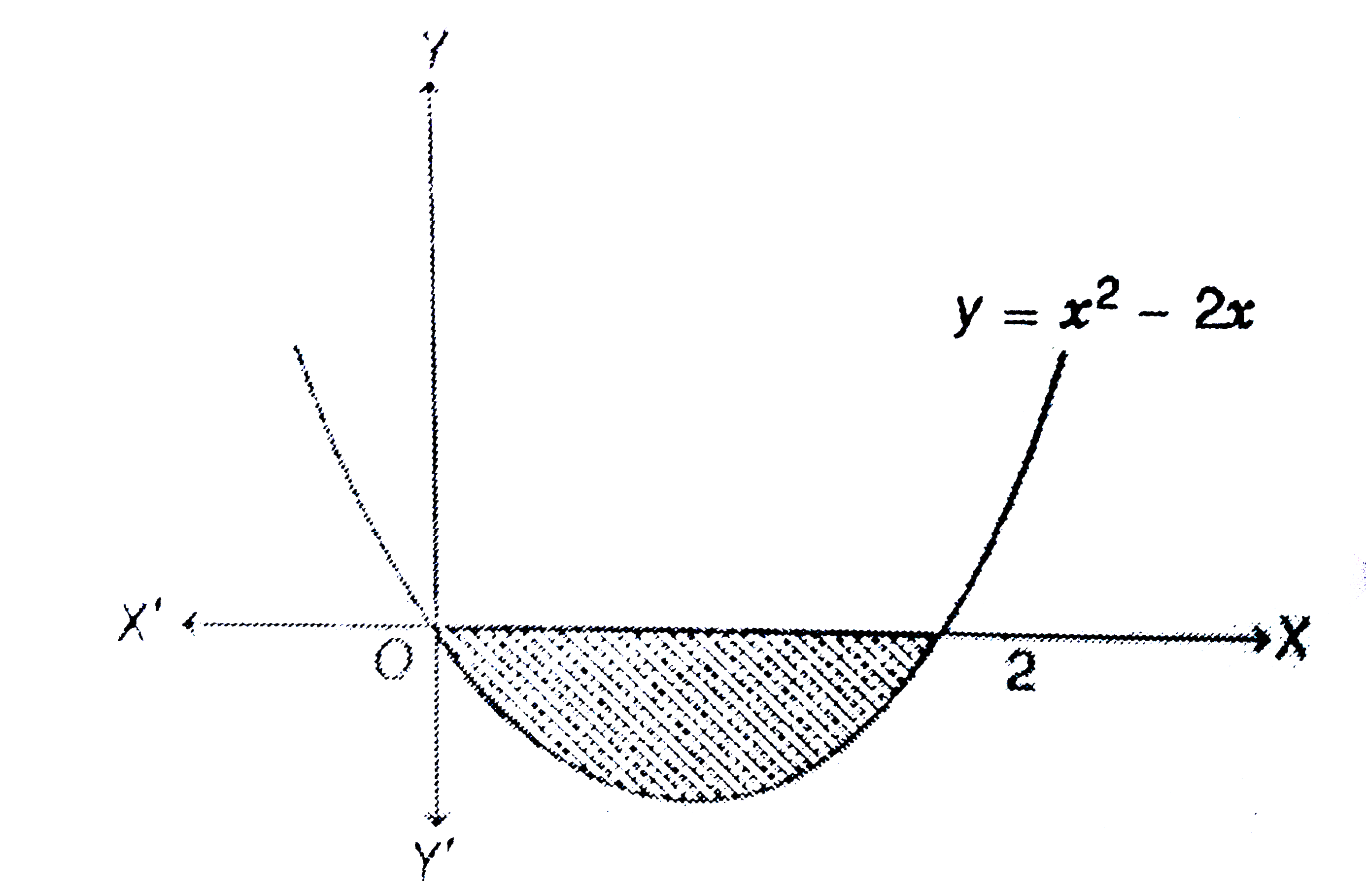
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A curve C passes through (2,0) and the slope at (x , y) as ((x+1)^2...
Text Solution
|
- Find the equation of the curve passing through the point (1,0) if t...
Text Solution
|
- A curve C passes through (2,0) and the slope at (x , y) as ((x+1)^2...
Text Solution
|
- Find the area bounded by the curve y=-3|x|+2 and x -axis
Text Solution
|
- Find the area bounded by the curve |x|+y=1 and axis of x.
Text Solution
|
- प्रथम चतुर्थांश में वक्र y ^(2) = 9x, x = 2, x = 4 एवं x -अ...
Text Solution
|
- A curve has a property that the slope of the tangent at a point (x, y)...
Text Solution
|
- वक्र |x| + y = 1 तथा x - अक्ष से घिरे हुए क्षेत्र का क्...
Text Solution
|
- बिन्दु (-2 ,3 ) से गुजरने वाले ऐसे वक्र का समीकरण ज्ञात कीजिए जिसके कि...
Text Solution
|