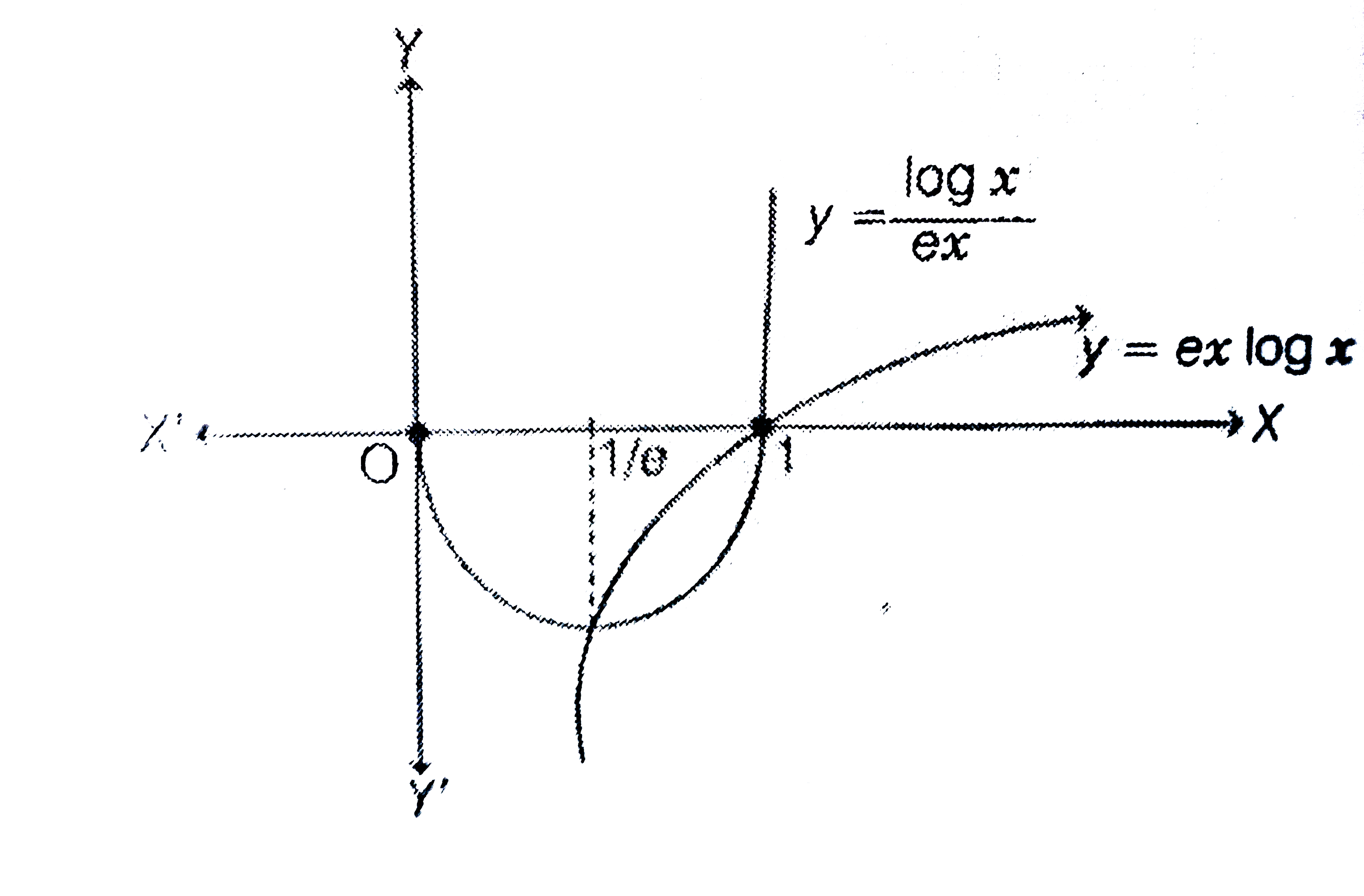Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Compute the area of the region bounded by the curves y=e x(loge x) and...
Text Solution
|
- Find the area bounded by y=loge x , y=-loge x ,y=loge(-x),a n dy=-loge...
Text Solution
|
- The area bounded by the curve y=2^(x), the x- axis and the left of y-a...
Text Solution
|
- Sketch the region bounded by the curves y=log(e)x and y=(log(e)x)^(2)....
Text Solution
|
- Draw the graph of y=log(e)(-x),-log(e)x,y=|log(e)x|,y=log(e)|x| and y=...
Text Solution
|
- The area (in sq units) of the region bounded by the curves y = e^(x), ...
Text Solution
|
- The area bounded by the curve y = log(e)x, the x-axis and the straight...
Text Solution
|
- वक्र y=log(e)x, X-अक्ष तथा कोटियों x = 1 तथा x = e से घिरे क्षेत्र का ...
Text Solution
|
- वक्रों y = e x log(e) x " और " y = (log(e)x)/(ex) घिरे क्षेत्र का क्ष...
Text Solution
|