Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
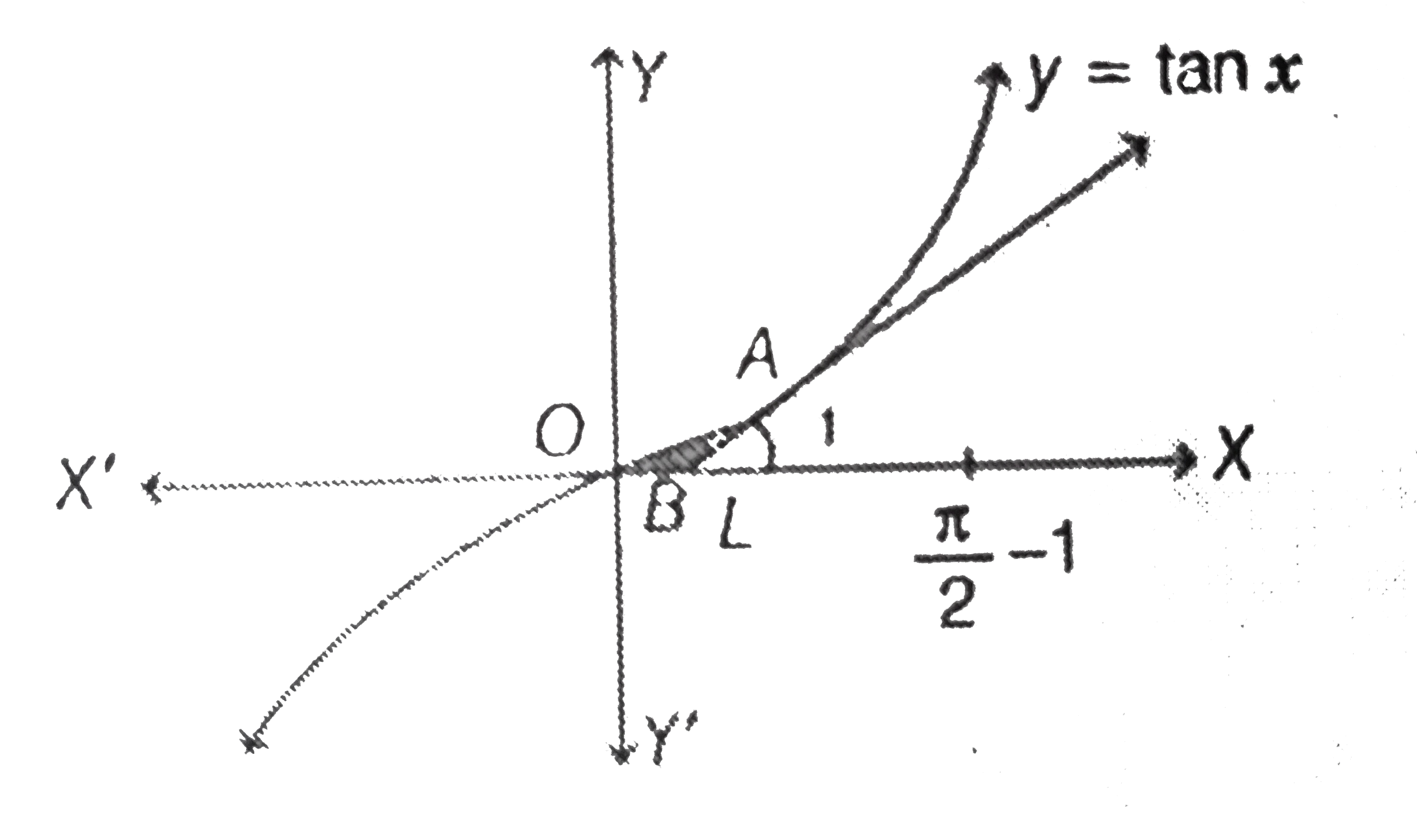
- Find the area of the region bounded by the curve C : y=tanx ,t a nge n...
Text Solution
|
- Find the area of the region bounded by the curve C:y=tan x, tangent dr...
Text Solution
|
- The area of the region bounded by the curve y=tan x, tangent drawn to ...
Text Solution
|
- Find the area of that region bounded by the curve y="cos"x, X-axis, x...
Text Solution
|
- Area bounded by the curves y = x ,y = tanx and x = pi/4 is
Text Solution
|
- Find the area of the region bounded by the curve y = sinx , ...
Text Solution
|
- वक्र y = cos x, ( 0 le x le pi ) तथा x -अक्ष से घिरे क्षेत्र का क्षेत...
Text Solution
|
- वक्र y=tanx का कोटियों x=-(pi)/4 तथा x=(pi)/4 से घिरे क्षेत्र का क्षेत...
Text Solution
|
- The area of the region bounded by the curve y=tanx tangent drawn to th...
Text Solution
|