Home
Class 12
MATHS
Sketch the region bounded by the curves ...

Sketch the region bounded by the curves `y=sqrt(5-x^(2)) and y=|x-1|` and find its area.

Text Solution

Verified by Experts

The correct Answer is:
`((5pi)/(4)-(1)/(2))` sq units
Given curves `y=sqrt(5-x^(2)) and y=|x-1|` could be sketched as shown, whose point of intersection are
`5-x^(2)=(x-1)^(2)`

`rArr 5-x^(2) =x^(2)-2x+1`
` 2x^(2) -2x-4=0`
`rArr x =2,-1`
`therefore ` Required area
`=int_(-1)^(2)sqrt(5-x^(2))dx -int_(-1)^(1)(-x+1)dx-int_(-1)^(1)(-x+1)dx -int_(1)^(2)(x-1)dx`
`=[(x)/(2) sqrt(5-x^(2))+(5)/(2) sin^(-1)((x)/(sqrt(5)))]_(-1)^(2)-[(-x^(2))/(2)+x]_(-1)^(1) -[(x^(2))/(2)-x]_(1)^(2)`
`=(1+(5)/(2)"sin"^(-1)(2)/(sqrt(5)))-[-1+(5)/(2)sin^(-1)((-1)/(sqrt(5)))]-(-(1)/(2)+1+(1)/(2)+1)-(2-2-(1)/(2)+1)`
`=(5)/(2)("sin"^(-1)(2)/(sqrt(5))+"sin"^(-1)(1)/(sqrt(5)))-(1)/(2)`
`=(5)/(2) sin^(-1)((2)/(sqrt(5)) sqrt(1-(1)/(5))+(1)/(sqrt(5))sqrt(1-(4)/(5)))-(1)/(2)`
`=(5)/(2) sin^(-1)(1)-(1)/(2)=((5pi)/(4)-(1)/(2))` sq units
Promotional Banner

Similar Questions

Explore conceptually related problems

Find the area bounded by the curves y=x^(3)-x and y=x^(2)+x.

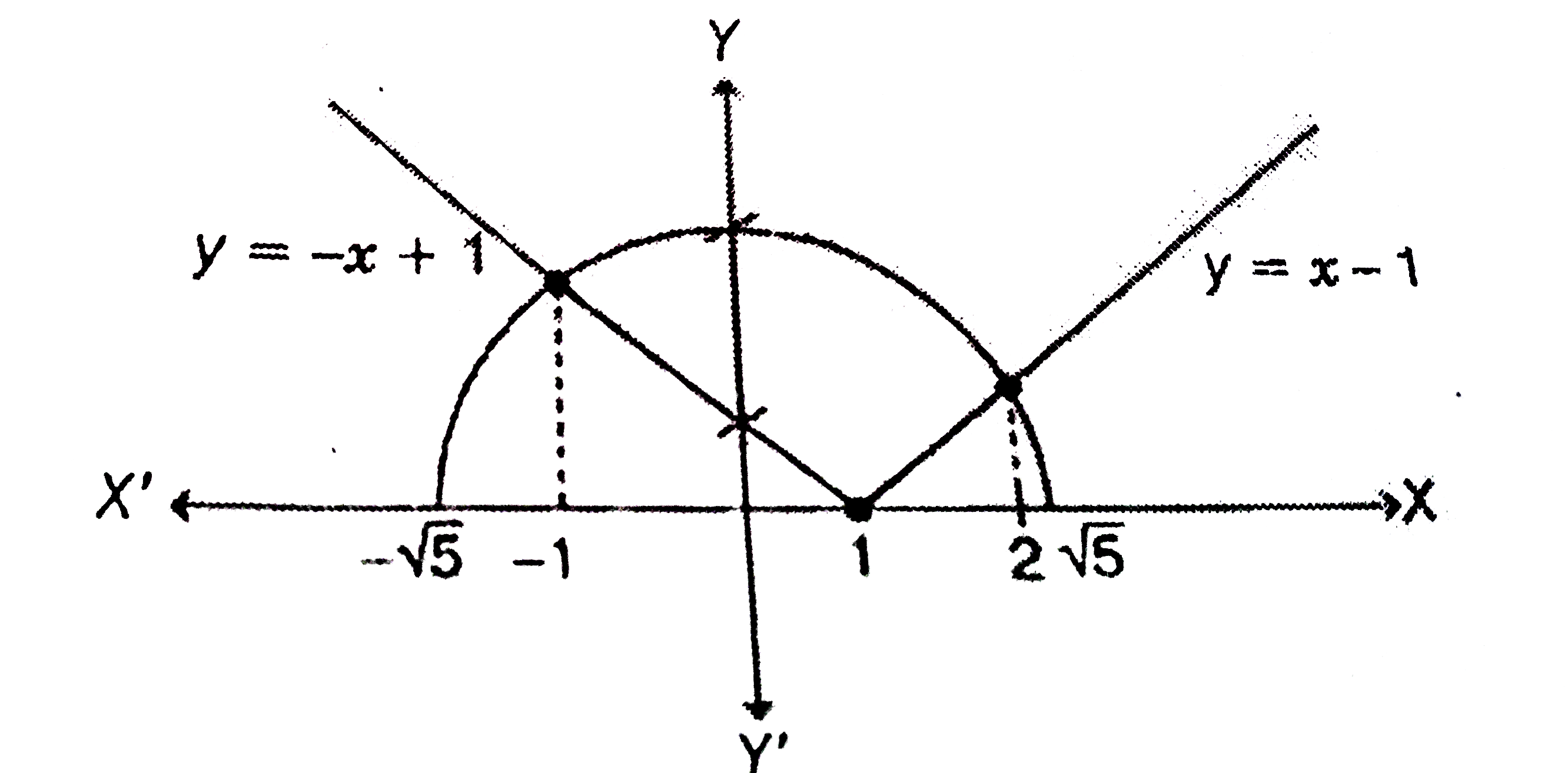
Sketch the region bounded by the curves y=x^2a n dy=2/(1+x^2) . Find the area.

Find the area bounded by the curves y=sqrt(1-x^(2)) and y=x^(3)-x without using integration.

If A is the area bounded by the curves y=sqrt(1-x^2) and y=x^3-x , then of pi/Adot

Find the area of the region bounded by the curves y=sqrt(x+2) and y=(1)/(x+1) between the lines x=0 and x=2.

Find the area bounded by the curve x=7 -6y-y^2 .

Area of the region bounded by the curve y=tanx and lines y = 0 and x = 1 is

The area of the region bounded by the curve y=e^(x) and lines x=0 and y=e is

The volume generated by the region bounded by the curve y=sqrt(x) and the line x=0 and x=pi about x axis is :