Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the area of the region bounded by the x-axis and the curves defin...
Text Solution
|
- Find the area of the region bounded by the x-axis and the curves defin...
Text Solution
|
- Find the area of the region bounded by the x-axis and the curves defi...
Text Solution
|
- The area of the region bounded by the X-axis and the curves defined by...
Text Solution
|
- वक्र y = cos x, ( 0 le x le pi ) तथा x -अक्ष से घिरे क्षेत्र का क्षेत...
Text Solution
|
- वह क्षेत्रफल ज्ञात कीजिए , जो x-अक्ष तथा y=tan x, - pi/3 le x le pi//...
Text Solution
|
- वक्र y= tanx तथा x-अक्ष से घिरे क्षेत्र का क्षेत्रफल (जहाँ - pi//3 le ...
Text Solution
|
- Find the area between x-axis and the curve y = cos x, (pi)/(2) le x le...
Text Solution
|
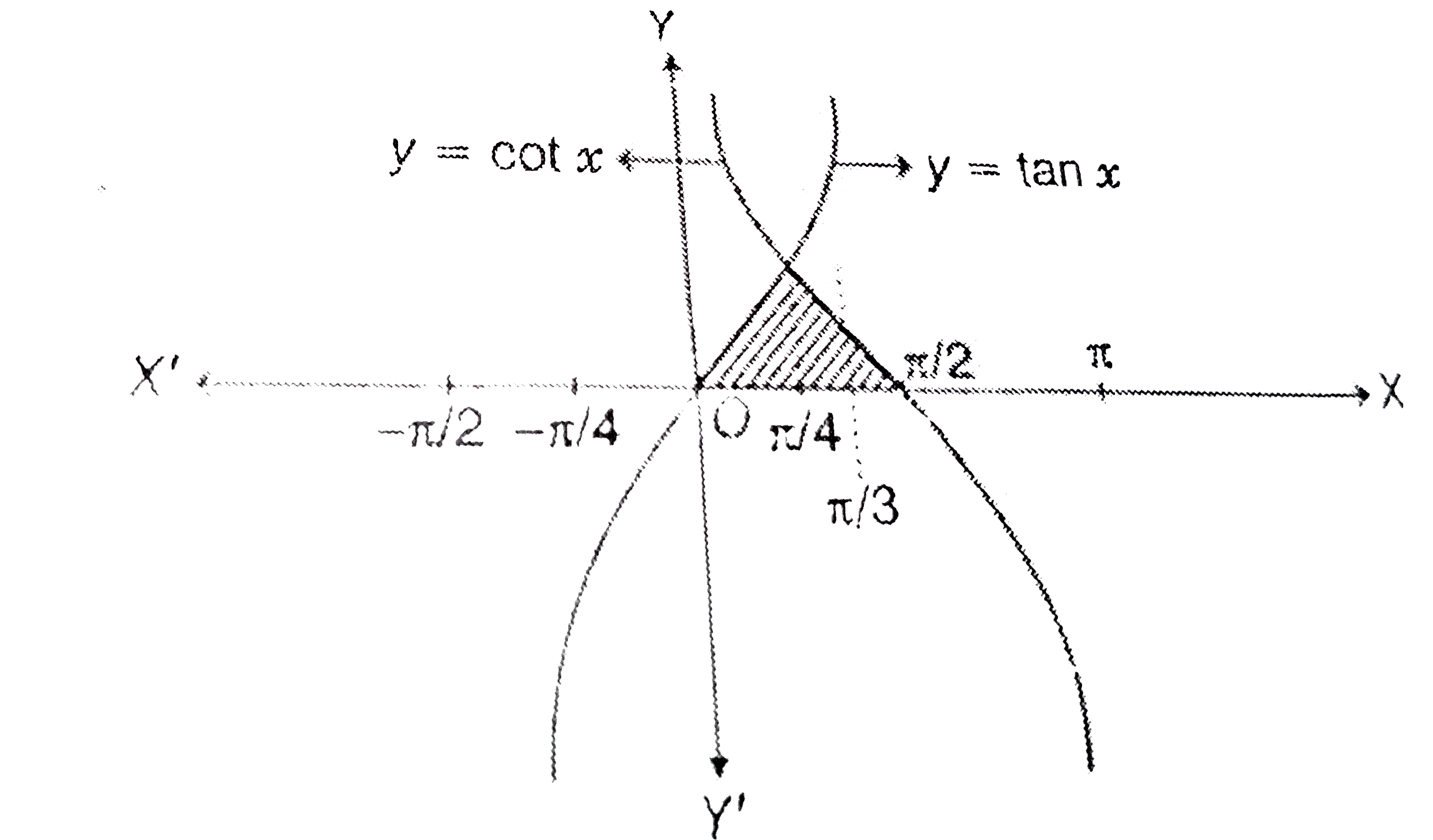
- The area bounded by the curves y=tanx, -(pi)/(3)le x le(pi)/(3),y=cotx...
Text Solution
|