Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
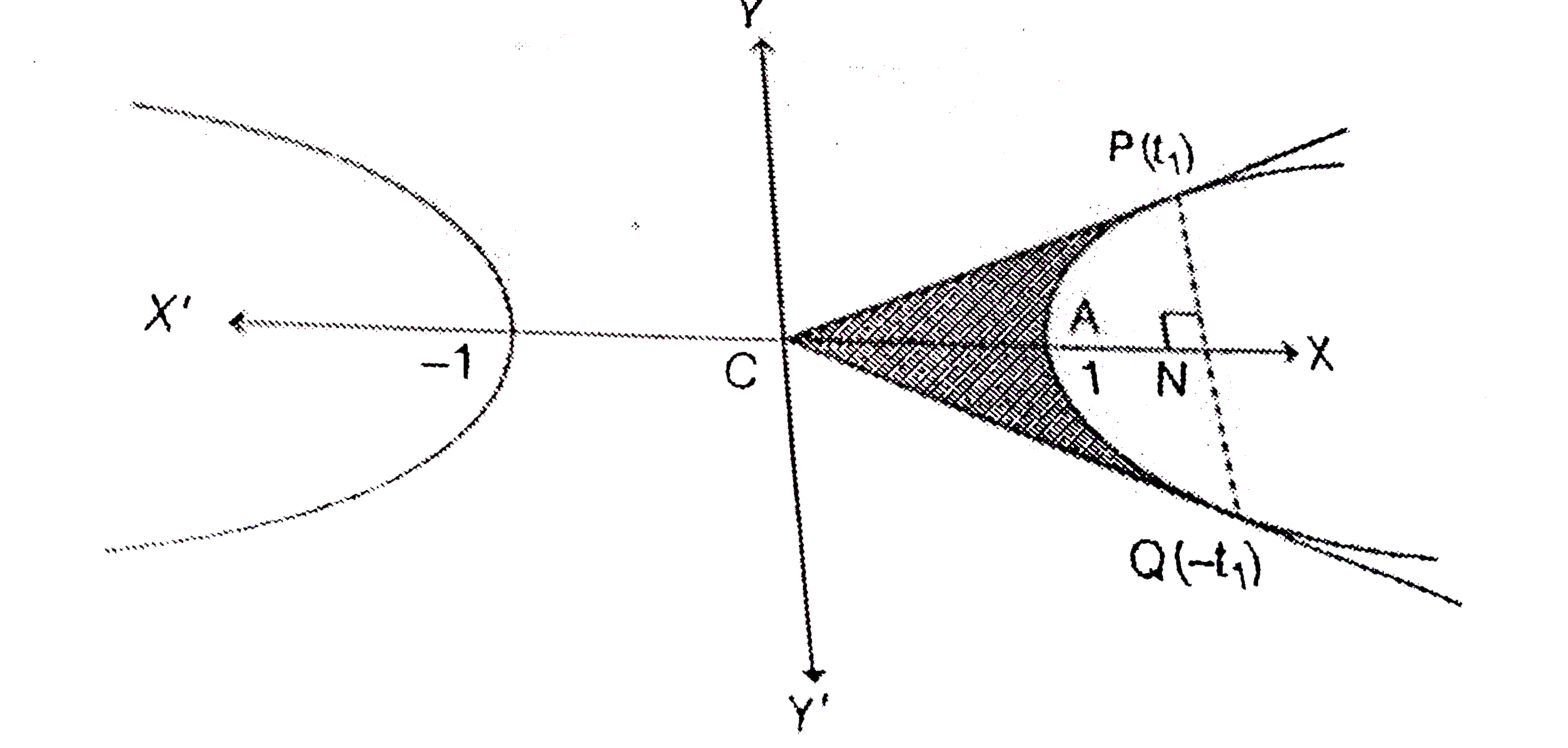
- For any real t ,x=1/2(e^t+e^(-t)),y=1/2(e^t-e^(-t)) is a point on the ...
Text Solution
|
- For any real t ,x=1/2(e^t+e^(-t)),y=1/2(e^t-e^(-t)) is a point on the ...
Text Solution
|
- Find the eccentricity of the hyperbola given by equations x=(e^t+e^(-1...
Text Solution
|
- The locus of point ((e^(t)+e^(-t))/(2),(e^(t)-e^(-t))/(2)) is a hyperb...
Text Solution
|
- The equation x = (e ^(t) + e ^(-t))/(2), y = (e ^(t) -e^(-t))/(2), t i...
Text Solution
|
- The locus of the point ( (e^(t) +e^(-t))/( 2),(e^t-e^(-t))/(2)) is a h...
Text Solution
|
- किसी वास्तविक t के लिए (x = e^(t) + e^(-t))/2, y = (e^(t) - e^(-t))/2...
Text Solution
|
- The equations x=(e^t+e^(-t))/2,y=(e^(t)-e^(-t))/2, t inR represent :
Text Solution
|
- Point ((e^t+e^(-t))/(2),(e^t-e^(-t))/(2)) The locus of is a hyperbola ...
Text Solution
|